题目内容
已知函数 (a∈R).
(a∈R).
(1)若 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
(2)若a=1,1≤x≤e,证明: <
< .
.
【答案】
解:(1)∵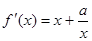 ,且在[1,e]上是增函数,∴
,且在[1,e]上是增函数,∴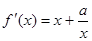 ≥0恒成立,
≥0恒成立,
即a≥-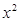 在[1,e]上恒成立, ∴a≥-1
在[1,e]上恒成立, ∴a≥-1
(2)证明:当a=1时,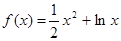 x∈[1,e].
x∈[1,e].
令F(x)= 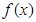 -
-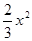 =
=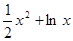 -
-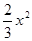 ,
,
∴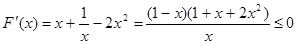 ,∴F(x) 在[1,e]上是减函数,
,∴F(x) 在[1,e]上是减函数,
∴F(x)≤F(1)= ∴x∈[1,e]时,
∴x∈[1,e]时,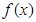 <
<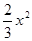
【解析】略

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).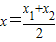 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围.