题目内容
(1)求与椭圆4x 2+9y 2=36 有相同的焦点,且过点(0,3)的椭圆方程.
(2)已知椭圆的对称轴为坐标轴,离心率e=
,长轴长为12,求椭圆的方程.
(2)已知椭圆的对称轴为坐标轴,离心率e=
| 2 | 3 |
分析:(1)所求的椭圆与椭圆
+
=1 有相同的焦点,可设
+
=1,(m>0).把(0,3)代入可得
=1,解得m即可.
(2)由题意可得
,解得a,b,c即可.
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| m+5 |
| y2 |
| m |
| 9 |
| m |
(2)由题意可得
|
解答:解:(1)∵所求的椭圆与椭圆
+
=1 有相同的焦点,∴可设
+
=1,(m>0).
把(0,3)代入可得
=1,解得m=9,
故所求的椭圆方程为
+
=1.
(2)由题意可得
,解得
.
故椭圆的方程为
+
=1或
+
=1.
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| m+5 |
| y2 |
| m |
把(0,3)代入可得
| 9 |
| m |
故所求的椭圆方程为
| x2 |
| 14 |
| y2 |
| 9 |
(2)由题意可得
|
|
故椭圆的方程为
| x2 |
| 36 |
| y2 |
| 20 |
| x2 |
| 20 |
| y2 |
| 36 |
点评:熟练掌握椭圆的标准方程及其性质是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
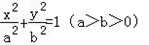 的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为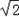 ,倾斜角为45°的直线l过点F.
,倾斜角为45°的直线l过点F.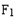 ,问抛物线y2=4x上是否存在一点M,使得M与
,问抛物线y2=4x上是否存在一点M,使得M与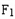 关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由.
关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由. ,长轴长为12,求椭圆的方程.
,长轴长为12,求椭圆的方程.