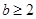题目内容
已知函数 ,若存在
,若存在 使得
使得 恒成立,则称
恒成立,则称 是
是 的
的
一个“下界函数” .
(I)如果函数 (t为实数)为
(t为实数)为 的一个“下界函数”,
的一个“下界函数”,
求t的取值范围;
(II)设函数 ,试问函数
,试问函数 是否存在零点,若存在,求出零点个数;
是否存在零点,若存在,求出零点个数;
若不存在,请说明理由.
【答案】
(I) (II)函数
(II)函数 不存在零点
不存在零点
【解析】
试题分析:(Ⅰ) 恒成立,
恒成立, ,
, ,
,
令 ,则
,则 ,
,
当 时,
时, ,
, 在
在 上是减函数,当
上是减函数,当 时,
时, ,
, 在
在
 上是增函数,
上是增函数,


(Ⅱ)由(I)知,

 ①,
①,
 ,
,
令 ,则
,则 ,
,
则 时,
时, ,
,  上是减函数,
上是减函数, 时,
时, ,
,
 上是增函数,
上是增函数, ②,
②,
 ,
, ①②中等号取到的条件不同,
①②中等号取到的条件不同, ,
,
 函数
函数 不存在零点.
不存在零点.
考点:导数在最大值、最小值问题中的应用;利用导数研究函数的极值.
点评:本题考查函数的最值的求法,利用函数的导函数求函数的最值,本题是一个综合题目,
可以作为高考卷的压轴题目,注意本题对于新定义的理解是解题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
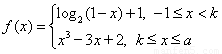




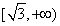



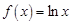 ,若存在
,若存在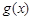 使得
使得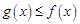 恒成立,则称
恒成立,则称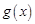 是
是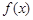 的一个“下界函数”
.
的一个“下界函数”
.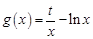 (
(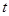 为实数)为
为实数)为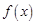 的一个“下界函数”,求
的一个“下界函数”,求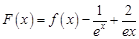 ,试问函数
,试问函数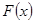 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由. 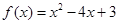 ,若存在
,若存在 使得
使得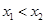 ,且
,且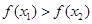 ,则以下对实数a、b的描述正确的是( ﹡
)
,则以下对实数a、b的描述正确的是( ﹡
)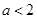 B.
B.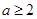 C.
C.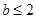 D.
D.