题目内容
已知点P是⊙O:x2+y2=9上的任意一点,过P作PD垂直于x轴于D,动点Q满足 ,
,
(1)求动点Q的轨迹方程;
(2)已知点E(1,1),在动点Q的轨迹上是否存在不重合的两点M,N,使 (O是坐标原点)?若存在,求出直线MN的方程;若不存在,请说明理由.
(O是坐标原点)?若存在,求出直线MN的方程;若不存在,请说明理由.
 ,
,(1)求动点Q的轨迹方程;
(2)已知点E(1,1),在动点Q的轨迹上是否存在不重合的两点M,N,使
 (O是坐标原点)?若存在,求出直线MN的方程;若不存在,请说明理由.
(O是坐标原点)?若存在,求出直线MN的方程;若不存在,请说明理由.解:(1)设P(x0,y0),Q(x,y),依题意,得点D的坐标为D(x0,0),
所以 ,
,
又 ,
,
所以 ,即
,即 ,
,
因为P在⊙O上,故 ,
,
所以 ,
,
所以Q点的轨迹方程为 。
。
(2)假设椭圆 上存在不重合的两点M(x1,y1),N(x2,y2)满足
上存在不重合的两点M(x1,y1),N(x2,y2)满足 ,
,
则E(1,1)是线段MN的中点,且有 ,即
,即 ,
,
又M(x1,y1),N(x2,y2)在椭圆 上,
上,
所以 ,
,
两式相减,得 ,
,
所以 ,
,
则直线MN的方程为4x+9y-13=0,
所以动点Q的轨迹上存在点M,N满足 ,
,
此时直线MN的方程为4x+9y-13=0.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
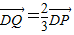 .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
.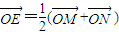 (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.