题目内容
已知点P是⊙O:x2+y2=9上的任意一点,过P作PD垂直x轴于D,动点Q满足| DQ |
| 2 |
| 3 |
| DP |
(1)求动点Q的轨迹方程;
(2)已知点E(1,1),在动点Q的轨迹上是否存在两个不重合的两点M、N,使
| OE |
| 1 |
| 2 |
| OM |
| ON |
分析:(1)设Q(x,y),利用向量的坐标运算,结合在⊙O上即可得到点Q的轨迹方程;
(2)对于存在性问题的解决方法,可假设存在.由向量关系式得E(1,1)是线段MN的中点,利用中点坐标公式及椭圆的方程式,得到直线MN的斜率值,从而求得直线的方程.结果表明存在.
(2)对于存在性问题的解决方法,可假设存在.由向量关系式得E(1,1)是线段MN的中点,利用中点坐标公式及椭圆的方程式,得到直线MN的斜率值,从而求得直线的方程.结果表明存在.
解答:解:(1)设P(x0,y0),Q(x,y),依题意,则点D的坐标为D(x0,0)(1分)
∴
=(x-x0,y),
=(0,y0)(2分)
又
=
∴
即
(4分)
∵P在⊙O上,故x02+y02=9∴
+
=1(5分)
∴点Q的轨迹方程为
+
=1(6分)
(2)假设椭圆
+
=1上存在两个不重合的两点M(x1,y1),N(x2,y2)满足
=
(
+
),则E(1,1)是线段MN的中点,且有
即
又M(x1,y1),N(x2,y2)在椭圆
+
=1上
∴
两式相减,得
+
=0(12分)
∴kMN=
=-
∴直线MN的方程为4x+9y-13=0
将直线MN的方程代入椭圆方程检验得:52x2-104x-155=0则△>0有实根
∴椭圆上存在点M、N满足
=
(
+
),此时直线MN的方程为4x+9y-13=0(14分)
∴
| DQ |
| DP |
又
| DQ |
| 2 |
| 3 |
| DP |
|
|
∵P在⊙O上,故x02+y02=9∴
| x2 |
| 9 |
| y2 |
| 4 |
∴点Q的轨迹方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)假设椭圆
| x2 |
| 9 |
| y2 |
| 4 |
| OE |
| 1 |
| 2 |
| OM |
| ON |
|
|
又M(x1,y1),N(x2,y2)在椭圆
| x2 |
| 9 |
| y2 |
| 4 |
∴
|
两式相减,得
| (x1-x2)(x1+x2) |
| 9 |
| (y1-y2)(y1+y2) |
| 4 |
∴kMN=
| y1-y2 |
| x1-x2 |
| 4 |
| 9 |
将直线MN的方程代入椭圆方程检验得:52x2-104x-155=0则△>0有实根
∴椭圆上存在点M、N满足
| OE |
| 1 |
| 2 |
| OM |
| ON |
点评:本题在向量与圆锥曲线交汇处命题,考查了向量的坐标运算、曲线方程的求法、椭圆的定义以及等价转化能力.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
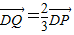 .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
. (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由. .
.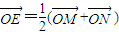 (O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.
(O是坐标原点),若存在,求出直线MN的方程,若不存在,请说明理由.