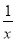��Ŀ����
Ϊ�����ļ����ºͶ�����ůʱ������Դ��ģ����ݵ��ݶ�����ǽ��Ҫ������Ȳ㣬ij��������Ҫ�����ʹ��20��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ6��Ԫ���ý�����ÿ�����Դ���ķ���C(��λ����Ԫ)����Ȳ���x(��λ��cm)�����ϵ��C(x)��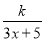 (0��x��10)�����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f(x)Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
(0��x��10)�����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f(x)Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
(1)��k��ֵ��f(x)�ı���ʽ��
(2)���Ȳ������ʱ���ܷ���f(x)�ﵽ��С��������Сֵ��
��1��f(x)��20�� ��6x��
��6x�� ��6x(0��x��10)��2��5 cm����70��Ԫ
��6x(0��x��10)��2��5 cm����70��Ԫ
��������(1)����Ȳ���x cm�������⣬������ÿ�����Դ���ķ���ΪC(x)�� (0��x��10)������C(0)��8����k��40��
(0��x��10)������C(0)��8����k��40��
��C(x)�� (0��x��10)���������Ȳ㽨�����Ϊ6x(��Ԫ)��
(0��x��10)���������Ȳ㽨�����Ϊ6x(��Ԫ)��
��f(x)��20�� ��6x��
��6x�� ��6x(0��x��10)��
��6x(0��x��10)��
(2)f(x)�� ��6x��
��6x�� ��(6x��10)��10��
��(6x��10)��10��
��0��x��10����6x��10��0����f(x)��2 ��10��70.
��10��70.
���ҽ��� ��6x��10.��x��5ʱ��ȡ�������ţ�
��6x��10.��x��5ʱ��ȡ�������ţ�
�ʸ��Ȳ���5 cm��ʱ���ܷ�����С����СֵΪ70��Ԫ��

��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�
�����Ŀ