题目内容
f(x)=3sin(ωx+ ),ω>0,x∈(-∞,+∞),且以
),ω>0,x∈(-∞,+∞),且以 为最小周期.
为最小周期.
(1)求f(0);
(2)求f(x)的解析式;
(3)已知f( +
+ )=
)= ,求sinα的值.
,求sinα的值.
解:(1)f(0)=3sin(ω•0+ )=3×
)=3× =
= ,
,
(2)∵T= ∴ω=4
∴ω=4
所以f(x)=3sin(4x+ ).
).
(3)f( +
+ )=3sin[4(
)=3sin[4( +
+ )+
)+ ]=3sin(
]=3sin(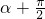 )=
)=
∴cosα=
∴sinα=
分析:(1)直接把x=0代入函数f(x)=3sin(ωx+ ),求f(0)即可;
),求f(0)即可;
(2)根据函数的周期求出ω,即可求f(x)的解析式;
(3)利用f( +
+ )=
)= ,化简求出cosα=
,化简求出cosα= ,利用三角函数的平方关系求sinα的值.
,利用三角函数的平方关系求sinα的值.
点评:本题是基础题,考查三角函数的值的求法,函数解析式的求法,三角函数基本关系式的应用,考查计算能力,常考题.
 )=3×
)=3× =
= ,
,(2)∵T=
 ∴ω=4
∴ω=4所以f(x)=3sin(4x+
 ).
).(3)f(
 +
+ )=3sin[4(
)=3sin[4( +
+ )+
)+ ]=3sin(
]=3sin(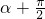 )=
)=
∴cosα=

∴sinα=

分析:(1)直接把x=0代入函数f(x)=3sin(ωx+
 ),求f(0)即可;
),求f(0)即可;(2)根据函数的周期求出ω,即可求f(x)的解析式;
(3)利用f(
 +
+ )=
)= ,化简求出cosα=
,化简求出cosα= ,利用三角函数的平方关系求sinα的值.
,利用三角函数的平方关系求sinα的值.点评:本题是基础题,考查三角函数的值的求法,函数解析式的求法,三角函数基本关系式的应用,考查计算能力,常考题.

练习册系列答案
相关题目
函数f(x)=3sin(x+100)+5sin(x+700)的最大值是( )
| A、5.5 | B、6.5 | C、7 | D、8 |