题目内容
设点P(x,y)在 所确定区域内,则点P(x,y)所在的区域面积为
所确定区域内,则点P(x,y)所在的区域面积为
- A.
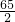
- B.65
- C.130
- D.169
C
分析:先根据约束条件 ,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.
,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.
解答: 解:当x≥0,y≥0时,
解:当x≥0,y≥0时, ;
;
当x≥0,y≤0时, -
- ≤1;
≤1;
当x≤0,y≥0时,- +
+ ≤1;
≤1;
当x≤0,y≤0时,- -
- ≤1;
≤1;
画出图形,如图所示.
点P(x,y)所在的区域面积为
S=4× ×5×13=130.
×5×13=130.
故选C.
点评:本题主要考查了简单线性规划的应用、二元一次不等式(组)与平面区域等知识,属于基础题.文科考查线性规划问题都考查的比较浅,难度不大这与理科有所区别,本题就具备这个特点.
分析:先根据约束条件
 ,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.
,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.解答:
 解:当x≥0,y≥0时,
解:当x≥0,y≥0时, ;
;当x≥0,y≤0时,
 -
- ≤1;
≤1;当x≤0,y≥0时,-
 +
+ ≤1;
≤1;当x≤0,y≤0时,-
 -
- ≤1;
≤1;画出图形,如图所示.
点P(x,y)所在的区域面积为
S=4×
 ×5×13=130.
×5×13=130.故选C.
点评:本题主要考查了简单线性规划的应用、二元一次不等式(组)与平面区域等知识,属于基础题.文科考查线性规划问题都考查的比较浅,难度不大这与理科有所区别,本题就具备这个特点.

练习册系列答案
相关题目
设点P(x,y)在|
|+|
|≤1所确定区域内,则点P(x,y)所在的区域面积为( )
| x |
| 5 |
| y |
| 13 |
A、
| ||
| B、65 | ||
| C、130 | ||
| D、169 |
 所表示的平面区域上运动,则z=x+y的最小值是 .
所表示的平面区域上运动,则z=x+y的最小值是 . 所确定区域内,则点P(x,y)所在的区域面积为( )
所确定区域内,则点P(x,y)所在的区域面积为( )