题目内容
 如图,已知四棱锥A-BCDE,其中AB=CD=2BE=2
如图,已知四棱锥A-BCDE,其中AB=CD=2BE=2| 2 |
(1)求证:EF∥平面ABC
(2)求直线BD与平面AED的夹角θ的正弦值.
分析:(1)要证线面平行,可在平面内找到一条与已知直线平行的线,由题目给出的F为AD的中点,可联想取AC中点G,连结BG后利用三角形的中位线和已知条件求证;
(2)由题意证出CB、BA、CD两两垂直,建系后借助于空间向量求解线面角的正弦值.
(2)由题意证出CB、BA、CD两两垂直,建系后借助于空间向量求解线面角的正弦值.
解答: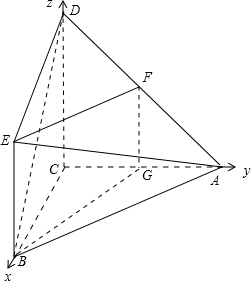 (1)证明:取AC中点G,连结FG,BG.
(1)证明:取AC中点G,连结FG,BG.
∵F为AD的中点,∴FG∥CD,FG=
CD.
又BE∥CD,BE=
CD,
∴四边形BGFE为平行四边形,∴EF∥BG.
EF?面ABC,BG?面ABC,∴EF∥平面ABC.
(2)解:∵AC=BC=2,AB=2
,AC2+BC2=AB2,∴AC⊥BC.
又CD⊥面ABC,∴CD⊥BC,CD⊥AC.
以C为坐标原点,以CB、CA、CD所在直线分别为x、y、z轴建立空间直角坐标系.
则B(2,0,0),D(0,0,2
),A(0,2,0),E(2,0,
).
∴
=(-2,0,2
),
=(0,-2,2
),
=(-2,0,
).
设平面AED的一个法向量为
=(x,y,z).
由
⇒
⇒
,
取z=1,得y=
,x=
.
∴
=(
,
,1).
∴直线BD与平面AED的夹角θ的正弦值
sinθ=|
|=|
|=
.
 (1)证明:取AC中点G,连结FG,BG.
(1)证明:取AC中点G,连结FG,BG.∵F为AD的中点,∴FG∥CD,FG=
| 1 |
| 2 |
又BE∥CD,BE=
| 1 |
| 2 |
∴四边形BGFE为平行四边形,∴EF∥BG.
EF?面ABC,BG?面ABC,∴EF∥平面ABC.
(2)解:∵AC=BC=2,AB=2
| 2 |
又CD⊥面ABC,∴CD⊥BC,CD⊥AC.
以C为坐标原点,以CB、CA、CD所在直线分别为x、y、z轴建立空间直角坐标系.
则B(2,0,0),D(0,0,2
| 2 |
| 2 |
∴
| BD |
| 2 |
| AD |
| 2 |
| ED |
| 2 |
设平面AED的一个法向量为
| m |
由
|
|
|
取z=1,得y=
| 2 |
| ||
| 2 |
∴
| m |
| ||
| 2 |
| 2 |
∴直线BD与平面AED的夹角θ的正弦值
sinθ=|
| ||||
|
|
-2×
| ||||||
|
| ||
| 21 |
点评:本题考查了空间中的线面平行的判定,考查了利用空间向量求解线面角,解答的关键是建立正确的空间右手系,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
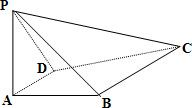 如图,已知四棱锥P-ABCD中,PA⊥平面CDAB,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.求点D到平面PBC的距离.
如图,已知四棱锥P-ABCD中,PA⊥平面CDAB,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2,PA=AB=1.求点D到平面PBC的距离.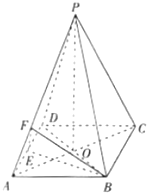 如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.
如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.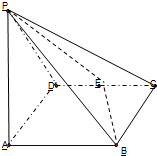 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成60°角.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成60°角. (2012•安徽模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2012•安徽模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.