题目内容
(文)长方体一条对角线与共顶点的三条棱所成的角分别为α,β,γ,则sin2α-cos2β-cos2γ=________.
0
分析:如图,在长方体AC1中,以AC1为斜边构成直角三角形,再结合长方体的对角线长定理,即可推出结论.
解答: 解:如图,在长方体AC1中,
解:如图,在长方体AC1中,
以AC1为斜边构成直角三角形:△AC1D,AC1B,AC1A1,
由长方体的对角线长定理可得
cos2α+cos2β+cos2γ
= .
.
则sin2α-cos2β-cos2γ=1-(cos2α+cos2β+cos2γ)=0
故答案为:0.
点评:本题考查棱柱的结构特征,考查长方体的对角线长定理的应用,是基础题.
分析:如图,在长方体AC1中,以AC1为斜边构成直角三角形,再结合长方体的对角线长定理,即可推出结论.
解答:
 解:如图,在长方体AC1中,
解:如图,在长方体AC1中,以AC1为斜边构成直角三角形:△AC1D,AC1B,AC1A1,
由长方体的对角线长定理可得
cos2α+cos2β+cos2γ
=
 .
.则sin2α-cos2β-cos2γ=1-(cos2α+cos2β+cos2γ)=0
故答案为:0.
点评:本题考查棱柱的结构特征,考查长方体的对角线长定理的应用,是基础题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 | A | B | C | D | E |
| 销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)对计算结果进行简要的分析说明.
 ;
;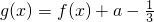 在区间[0,5]上没有零点,求实数a的取值范围.
在区间[0,5]上没有零点,求实数a的取值范围. ,若f(m)+f(n)=1,则f(m•n)的最小值为
,若f(m)+f(n)=1,则f(m•n)的最小值为



 ;②
;② ;③
;③ ;④
;④ .正确命题的序号为________(注:把你认为正确的序号都填上).
.正确命题的序号为________(注:把你认为正确的序号都填上). 的定义域为(0,+∞)(a为实数).
的定义域为(0,+∞)(a为实数). 已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C.