Question

A是圆x²+y²=r²(r＞0)上任意一点,AB⊥x轴于B,以A为圆心,|AB|为半径的圆,交已知圆于C、D两点,连结CD交AB于M点,当点A在圆上运动时,求点M的轨迹方程.

Answer 1

思路解析：动点A落在x轴上时,|AB|=0,A、M重合于(±r,0);点A落在y轴上时,|AB|=r,有A(0,±r).由此可知:点M的轨迹是以r为长半轴,为短半轴,且中心在原点的椭圆,求轨迹方程的方法,应选择转移、交轨法.

解：设圆上动点A(x₀,y₀),那么x₀²+y₀²=r²,以A为圆心,|AB|=|y₀|为半径的圆的方程为(x-x₀)²+(y-y₀)²=y₀².

由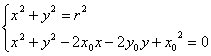2x₀x+2y₀y=r²+x₀²,

此即弦CD所在直线的方程.

设点M的坐标为(x,y),因为AB⊥x轴,有x=x₀,代入CD的方程2x₀x+2y₀y=r²+x₀²,可得2y₀y=r²-x₀²=y₀²,得y₀=2y.

将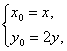代入x₀²+y₀²=r²,可得x²+4y²=r².

此即为所求轨迹方程,可化为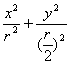=1,表示以2r为长轴,r为短轴的椭圆.