题目内容
(本小题满分12分)已知命题 :在
:在 上定义运算
上定义运算 :
: 不等式
不等式 对任意实数
对任意实数 恒成立;命题
恒成立;命题 :若不等式
:若不等式 对任意的
对任意的 恒成立.若
恒成立.若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.

【解析】
试题分析:根据题意,将各个命题为真命题时对应的参数的取值范围先求出来,再根据复合命题的真值,可以断定两个命题中真命题的个数,从而求得对应的结果.
试题解析:由题意知,
若命题 为真,
为真, 对任意实数
对任意实数 恒成立, 1分
恒成立, 1分
 ①当
①当 即
即 时,
时, 恒成立,
恒成立, ; 2分
; 2分
②当 时,
时, ,
, , 3分
, 3分
综合①②得, 4分
4分
若命题 为真,
为真, ,
, ,
,
则有 对任意的
对任意的 恒成立 , 5分
恒成立 , 5分
即 对任意的
对任意的 恒成立,
恒成立,
令 ,只需
,只需 , 6分
, 6分
 ,当且仅当
,当且仅当 即
即 时取“=”
时取“=”
 8分
8分

 为假命题,
为假命题, 为真命题,
为真命题, 中必有一个真命题,一个假命题, 9分
中必有一个真命题,一个假命题, 9分
(1)若 为真
为真 为假,则
为假,则 ,
, , 10分
, 10分
(2)若 为假
为假 为真,则
为真,则 ,
, , 11分
, 11分
综上: 12分
12分
考点:复合命题的真值表,恒成立问题.
考点分析: 考点1:命题及其关系 考点2:简单的逻辑联结词 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
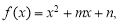 若
若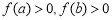 ,则函数
,则函数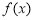 在区间
在区间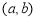 内
内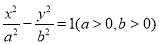 ,F是双曲线C的右焦点,点A是渐近线上第一象限内的一点,O为坐标原点,且|OA|=
,F是双曲线C的右焦点,点A是渐近线上第一象限内的一点,O为坐标原点,且|OA|=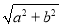 ,若
,若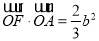 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )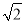 B.
B.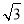 C.2 D.
C.2 D.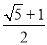
 B.
B. C.
C. D.
D.
 中,满足
中,满足 ,且
,且 ,
, 是其前
是其前 项和,若
项和,若 的解集为 ( )
的解集为 ( )  B.
B. C.
C. D.
D.
 的解集为 .
的解集为 .

 ,
, )
)