题目内容
(1)求过点M(2,4)向圆(x-1)2+(y+3)2=1 所引的切线方程；(2)过点M(2,4)向圆引两条切线，切点为P、Q，求P、Q所在直线方程(简称切点弦).
剖析：(1)用点斜式设直线方程时，要分斜率存在、不存在两种情况讨论；
(2)点M、圆心C、切点P、Q四点共圆，直线PQ为两圆公共弦，两圆方程相减即得公共弦方程.
解：(1)当所求切线斜率存在时，设切线方程为y-4=k(x-2)，即kx-y+4-2k=0.
∴
=1.解得k=
，
即切线方程为24x-7y-20=0.
当k不存在时，切线方程为x=2.
故所求切线方程为24x-7y-20=0或x=2.
(2)连结CP、CQ，则CP⊥PM，CQ⊥QM.
∴M、P、Q、C四点共圆.
其圆是以CM为直径的圆.
∵C(1,-3),∴CM的中点为(
,
).
|CM|=
=5
.
∴以CM为直径的圆的方程为(x-
)2+(y-
)2=
.
∴PQ的方程为(x-1)2+(y+3)2-1-［(x-
)2+(y-
)2-
］=0，即x+7y+19=0.
练习册系列答案
相关题目
.
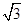的直线方程．
.
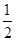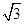的直线方程．
. (1)求圆C的方程。（2）点P(x,y)是圆C上的动点，求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
. (1)求圆C的方程。（2）点P(x,y)是圆C上的动点，求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。