题目内容
已知点P与两个定点O(0,0),A(-3,0)距离之比为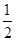 .
.
(1)求点P的轨迹C方程;
(2)求过点M(2,3)且被轨迹C截得的线段长为2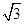 的直线方程.
的直线方程.
【答案】
(1)x²+y²-2x-3=0.(2)直线l的方程为3x+4y-8=0或x=1.
【解析】
试题分析:解:(1)设点P(x,y),则依题得|MA|=2|MO|,
∴ =2
=2 ,
,
整理得x²+y²-2x-3=0,
∴轨迹C方程为x²+y²-2x-3=0. 4分
(2)圆的方程可化为(x-1)²+y²=4,则:
圆心为(1,0),半径为2,
∵直线l过点P且被圆截得的线段长为2,
∴弦心距为d= =1.
=1.
设直线l的方程为y=k(x-2)+3即k(x-2)-y+3=0,
∴ =1,解得k=
=1,解得k= .
7分
.
7分
∴此时直线的方程为y= (x-2)+3即4x-3y+1=0.
(x-2)+3即4x-3y+1=0.
又当直线的斜率不存在时,直线的方程为x=1.经检验,直线x=-4也符合题意.
∴直线l的方程为3x+4y-8=0或x=1. 9分
考点:直线与圆的位置关系
点评:主要是考查了直线与圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
 .
.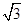 的直线方程.
的直线方程.