题目内容
(本小题满分13分)椭圆 的左、右焦点分别是
的左、右焦点分别是 ,
, ,过
,过 斜率为1的直线与椭圆
斜率为1的直线与椭圆 相交于
相交于 ,
, 两点,且
两点,且 ,
, ,
, 成等差数列.
成等差数列.
(1)请探求 与
与 的关系;
的关系;
(2)设点 在线段
在线段 的垂直平分线上,求椭圆
的垂直平分线上,求椭圆 的方程.
的方程.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先根据椭圆的定义得到 的周长为
的周长为 ,进而结合
,进而结合 ,
, ,
, 成等差数列得出
成等差数列得出 ,然后联立直线与椭圆的方程,消去
,然后联立直线与椭圆的方程,消去 ,得到
,得到 ,进而得出
,进而得出 ,再利用弦长公式计算出
,再利用弦长公式计算出 ,化简
,化简 即可得出
即可得出 的关系;(2)结合(1)中得出的关系,得到
的关系;(2)结合(1)中得出的关系,得到 中点
中点 的坐标,然后根据
的坐标,然后根据 ,即可计算出
,即可计算出 的取值,写出椭圆的方程即可.
的取值,写出椭圆的方程即可.
试题解析:(1)由题设,得

 , 由椭圆定义
, 由椭圆定义

 ,所以
,所以 .
.
设 ,
, ,
, ,
, ,代入椭圆
,代入椭圆 的方程
的方程
整理得 (*)
(*)
所以
则

于是有 ,化简,得
,化简,得 ,故
,故
(2)由(1)有 ,方程(*)可化为
,方程(*)可化为
设 中点为
中点为 ,则
,则
又 ,于是
,于是 . 由
. 由
 知
知 为
为 的中垂线,
的中垂线,
由 ,得
,得 ,解得
,解得 ,
,
故椭圆 的方程为
的方程为 .
.
考点:1.椭圆的定义;2.椭圆的标准方程及其几何性质;3.二次方程根与系数的关系;4.两直线垂直的充要条件.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,
, ,则下列不等式成立的是( )
,则下列不等式成立的是( ) B、
B、 C、
C、 D、
D、
 ( )
( ) 上单调递增
上单调递增  ,
, 是双曲线
是双曲线
 ,
, 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点 ,使
,使 (
( 为坐标原点),且
为坐标原点),且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) B.
B. C.
C. D.
D.
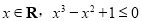 ”的否定是( )
”的否定是( )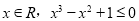

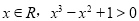

 中,
中, .如果一个椭圆通过
.如果一个椭圆通过 、
、 两点,它的一个焦点为点
两点,它的一个焦点为点 ,另一个焦点在边
,另一个焦点在边 上,则这个椭圆的焦距为 .
上,则这个椭圆的焦距为 .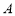 ,
,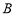 ,线段
,线段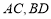 分别在这个二面角的两个面内,并且都垂直于棱
分别在这个二面角的两个面内,并且都垂直于棱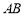 ,
,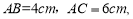
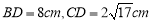 ,则这个二面角的度数为( )
,则这个二面角的度数为( )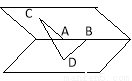
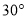 B.
B.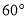 C.
C.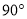 D.
D.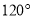
 ,其中
,其中 .
. 的最小值;
的最小值; 对任意的
对任意的 ,总有
,总有 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.