题目内容
已知各项都不为零的数列{an}满足an+1=| an |
| 1+an |
| 1 |
| 4 |
(Ⅰ) 求证数列{
| 1 |
| an |
(Ⅱ) 若c1=1,(n+3)cn+1=(n+2)cn,Sn=c1a2+c2a3+…+cnan+1,求Sn的最小值.
分析:(Ⅰ)、根据题中已知条件可以推导出
-
=1,即可证明数列{
}是等差数列,将a1=
代入等差数列
中即可求得数列{an}的通项公式;
(Ⅱ)、根据题中已知条件先求出cn的表达式,然后求出cnan+1的表达式,即可求出Sn的表达式,有Sn的表达式可知当n=1时,Sn的最小值.
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| 4 |
| 1 |
| an |
(Ⅱ)、根据题中已知条件先求出cn的表达式,然后求出cnan+1的表达式,即可求出Sn的表达式,有Sn的表达式可知当n=1时,Sn的最小值.
解答:解:(Ⅰ)由an+1=
,
∴
=
+1,即
-
=1,(2分)
∴{
}是首项为
,公差为1的等差数列,(3分)
∴
=
+(n-1)×1=4+(n-1)×1=n+3
∴an=
,(4分)
(Ⅱ)∵(n+3)cn+1=(n+2)cn,
∴
=
,
∴cn=
×
×
××
×c1
=
×
×
×
×1=
,(6分)
∴cnan+1=
=
(
-
),(8分)
∴Sn=c1a2+c2a3+…+cnan+1
=
[(
-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=
[(
+
-
-
)]
=
-
(
+
),(10分)
∵Sn在(0,+∞)上是增函数,(11分)
∴当n=1时,Sn有最小值为S1=
.(12分)
| an |
| 1+an |
∴
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
∴{
| 1 |
| an |
| 1 |
| a1 |
∴
| 1 |
| an |
| 1 |
| a1 |
∴an=
| 1 |
| n+3 |
(Ⅱ)∵(n+3)cn+1=(n+2)cn,
∴
| cn+1 |
| cn |
| n+2 |
| n+3 |
∴cn=
| c2 |
| c1 |
| c3 |
| c2 |
| c4 |
| c3 |
| cn |
| cn-1 |
=
| 3 |
| 4 |
| 4 |
| 5 |
| 5 |
| 6 |
| n+1 |
| n+2 |
| 3 |
| n+2 |
∴cnan+1=
| 3 |
| (n+2)(n+4) |
| 3 |
| 2 |
| 1 |
| n+2 |
| 1 |
| n+4 |
∴Sn=c1a2+c2a3+…+cnan+1
=
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| n+1 |
| 1 |
| n+3 |
| 1 |
| n+2 |
| 1 |
| n+4 |
=
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+3 |
| 1 |
| n+4 |
=
| 7 |
| 8 |
| 3 |
| 2 |
| 1 |
| n+3 |
| 1 |
| n+4 |
∵Sn在(0,+∞)上是增函数,(11分)
∴当n=1时,Sn有最小值为S1=
| 1 |
| 5 |
点评:本题考查了数列的求和和数列的推导公式,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的前
的前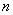 项和为
项和为 ,如果
,如果 为常数,则称数列
为常数,则称数列 的首项为1,公差不为零,若
的首项为1,公差不为零,若 的各项都是正数,前
的各项都是正数,前 对任意
对任意 都成立,试推断数列
都成立,试推断数列