题目内容
设数列 的前
的前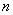 项和为
项和为 ,如果
,如果 为常数,则称数列
为常数,则称数列 为“科比数列”.
为“科比数列”.
(Ⅰ)已知等差数列 的首项为1,公差不为零,若
的首项为1,公差不为零,若 为“科比数列”,求
为“科比数列”,求 的通项公式;
的通项公式;
(Ⅱ)设数列 的各项都是正数,前
的各项都是正数,前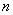 项和为
项和为 ,若
,若 对任意
对任意 都成立,试推断数列
都成立,试推断数列 是否为“科比数列”?并说明理由.
是否为“科比数列”?并说明理由.
【答案】
(Ⅰ)设等差数列 的公差为
的公差为 ,
, ,因为
,因为 ,则
,则
 ,即
,即 . (2分)
. (2分)
整理得, .
(3分)
.
(3分)
因为对任意正整数 上式恒成立,则
上式恒成立,则 ,解得
,解得 .
(5分)
.
(5分)
故数列 的通项公式是
的通项公式是 .
(6分)
.
(6分)
(Ⅱ)由已知,当 时,
时, .因为
.因为 ,所以
,所以 .
(7分)
.
(7分)
当 时,
时, ,
, .
.
两式相减,得 .
.
因为 ,所以
,所以 =
= .
(9分)
.
(9分)
显然 适合上式,所以当
适合上式,所以当 时,
时, .
.
于是 .
.
因为 ,则
,则 ,所以数列
,所以数列 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
所以 不为常数,故数列
不为常数,故数列 不是“科比数列”. (13分)
不是“科比数列”. (13分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
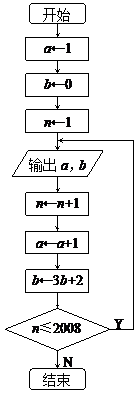 根据如图所示的流程图,将输出的
根据如图所示的流程图,将输出的 :
: 上一点
上一点 作曲线
作曲线 交
交 轴于点
轴于点 ,又过
,又过 作
作  ,然后再过
,然后再过 交
交 ,又过
,又过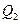 作
作 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 ,再过点
,再过点 作
作 (
( N
N ).
).
 、
、 及数列
及数列 的通项公式;
的通项公式;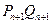 所围成的图形面积为
所围成的图形面积为 ,求
,求 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N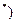 .
. ,其中
,其中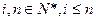 ,如
,如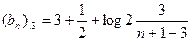 ,令
,令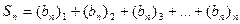 .
.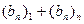 的值;
的值; 的表达式;
的表达式; 满足
满足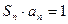 ,设数列
,设数列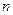 项和为
项和为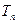 ,若对一切
,若对一切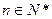 ,不等式
,不等式 恒成立,求实数
恒成立,求实数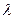 的最大值.
的最大值.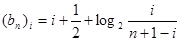 ,其中
,其中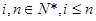 ,如
,如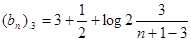 ,令
,令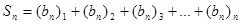 .
.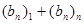 的值;
的值;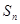 的表达式;
的表达式;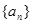 满足
满足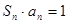 ,设数列
,设数列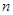 项和为
项和为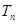 ,若对一切
,若对一切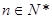 ,不等式
,不等式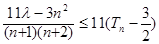 恒成立,求实数
恒成立,求实数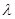 的最大值.
的最大值.