题目内容
甲乙两地相距400千米,汽车从甲地匀速行驶到乙地,速度不得超过100千米/小时,已知该汽车每小时的运输成本P(元)关于速度v(千米/小时)的函数关系是P=
v4-
v3+15v,
(1)求全程运输成本Q(元)关于速度v的函数关系式;
(2)为使全程运输成本最少,汽车应以多少速度行驶?并求此时运输成本的最小值.
| 1 |
| 19200 |
| 1 |
| 160 |
(1)求全程运输成本Q(元)关于速度v的函数关系式;
(2)为使全程运输成本最少,汽车应以多少速度行驶?并求此时运输成本的最小值.
(1)Q=P•
=(
v4-
v3+15v)•
=(
v3-
v2+15)•400
=
-
v2+6000(0<v≤100).
(2)Q′=
-5v,
令Q′=0,则v=0(舍去)或v=80,
当0<v<80时,Q′<0.
当80<v≤100时,Q′>0.
∴v=80时,全程运输成本取得极小值,即最小值.
从而Qmin=Q(80)=
元.
| 400 |
| v |
| 1 |
| 19200 |
| 1 |
| 160 |
| 400 |
| v |
=(
| 1 |
| 19200 |
| 1 |
| 160 |
=
| v3 |
| 48 |
| 5 |
| 2 |
(2)Q′=
| v2 |
| 16 |
令Q′=0,则v=0(舍去)或v=80,
当0<v<80时,Q′<0.
当80<v≤100时,Q′>0.
∴v=80时,全程运输成本取得极小值,即最小值.
从而Qmin=Q(80)=
| 2000 |
| 3 |

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
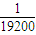 v4-
v4-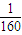 v3+15v,
v3+15v,