题目内容
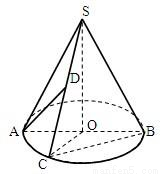
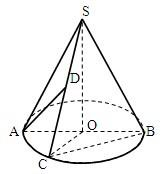 如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.(1)求证:BC与SA不可能垂直;
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为
| ||
| 6 |
分析:(1)法一应用反证法,若 BC⊥SA,推出∠SCB是锐角与BC⊥SC矛盾.
法二建立空间直角坐标系,求
•
=r2≠ 0说明两条直线不垂直.
(2)利用空间直角坐标系数量积求出底面半径,然后求体积.
法二建立空间直角坐标系,求
| SA |
| BC |
(2)利用空间直角坐标系数量积求出底面半径,然后求体积.
解答: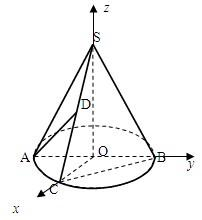 解:(1)证法一:反证法:若 BC⊥SA,
解:(1)证法一:反证法:若 BC⊥SA,
连AC,由AB是直径
则AC⊥BC,所以 BC⊥平面SAC
则 BC⊥SC
又圆锥的母线长相等,
∠SCB是等腰三角形SBC的底角,
则∠SCB是锐角
与BC⊥SC矛盾,所以BC与SA不垂直
证法二:建立如图坐标系,设圆锥的高为h,
底面半径为r,
则 B(0,r,0),C(r,0,0),A(0,-r,0)
S(0,0,h),
=(0,-r,-h),
=(r,-r,0),
•
= r2≠ 0,
所以BC与SA不垂直.
(2)建立如图坐标系,设底面半径为r,
由高为4.则 D(
,0,2),则
=(
,r,2),
=(r,-r,0)
cos<
,
>=
=
=
,
解得 r=2,
所以V=
πr2h=
.
 解:(1)证法一:反证法:若 BC⊥SA,
解:(1)证法一:反证法:若 BC⊥SA,连AC,由AB是直径
则AC⊥BC,所以 BC⊥平面SAC
则 BC⊥SC
又圆锥的母线长相等,
∠SCB是等腰三角形SBC的底角,
则∠SCB是锐角
与BC⊥SC矛盾,所以BC与SA不垂直
证法二:建立如图坐标系,设圆锥的高为h,
底面半径为r,
则 B(0,r,0),C(r,0,0),A(0,-r,0)
S(0,0,h),
| SA |
| BC |
| SA |
| BC |
所以BC与SA不垂直.
(2)建立如图坐标系,设底面半径为r,
由高为4.则 D(
| R |
| 2 |
| AD |
| r |
| 2 |
| BC |
cos<
| AD |
| BC |
-
| ||||||
|
| -r2 | ||||
|
| ||
| 6 |
解得 r=2,
所以V=
| 1 |
| 3 |
| 16π |
| 3 |
点评:本题考查组合体及旋转体的体积,空间直角坐标系,直线与平面所成的角,考查反证法,是中档题.

练习册系列答案
相关题目
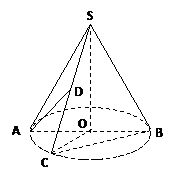 (2)设圆锥的高为4,异面直线AD与BC所成角为
(2)设圆锥的高为4,异面直线AD与BC所成角为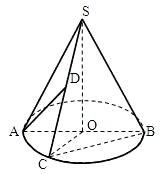 如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点. ,求圆锥的体积.
,求圆锥的体积.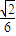 ,求圆锥的体积.
,求圆锥的体积.
 ,求圆锥的体积.
,求圆锥的体积.