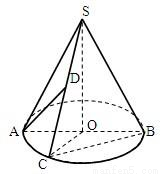
题目内容
如图:圆锥的顶点是S,底面中心为O。OC是与底面直径AB垂直的一条半径,D是母线SC的中点。
(1)求证:BC与SA不可能垂直;
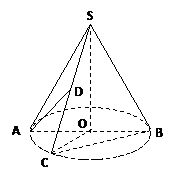 (2)设圆锥的高为4,异面直线AD与BC所成角为
(2)设圆锥的高为4,异面直线AD与BC所成角为![]() ,求圆锥的体积。
,求圆锥的体积。
见解析
解析:
解:(1)
证法一:反证法:若![]() ,连AC,由AB是直径
,连AC,由AB是直径
则![]() ,所以
,所以![]() 平面
平面![]() 2分
2分
则![]() 3分
3分
又圆锥的母线长相等,![]() 是等腰三角形SBC的底角,
是等腰三角形SBC的底角,
则![]() 是锐角 4分
是锐角 4分
与![]() 矛盾,所以
矛盾,所以![]() 与SA不垂直 6分
与SA不垂直 6分
证法二:建立如图坐标系,设圆锥的高为![]() ,底面
,底面
半径为![]() ,则
,则![]()
![]() ,
,![]() 3分
3分
![]() 5分
5分
所以![]() 与SA不垂直 6分
与SA不垂直 6分
(2)建立如图坐标系,设底面半径为![]() ,由高为4。则
,由高为4。则![]() ,则
,则![]() ,
,

![]() 8分
8分
 10分
10分
由AD与BC所成角为![]() ,所以
,所以![]() ,解得
,解得![]() 12分
12分
所以![]() 14分
14分

练习册系列答案
相关题目
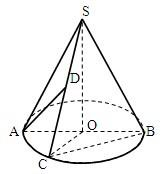 如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.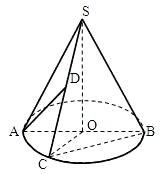 如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点. ,求圆锥的体积.
,求圆锥的体积.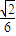 ,求圆锥的体积.
,求圆锥的体积.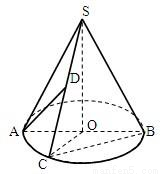
 ,求圆锥的体积.
,求圆锥的体积.