题目内容
若函数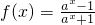 (a>0且a≠1).
(a>0且a≠1).
(1)判断f(x)的奇偶性;
(2)当a>1时,判断f(x)在(-∞,+∞)上的单调性,并加以证明.
(1)解:由f(x)的定义域为(-∞,+∞),关于数0对称(2分)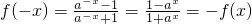 ,得∴f(x)为R上的奇函数.(6分)
,得∴f(x)为R上的奇函数.(6分)
(2)当a>1时,f(x)在(-∞,+∞)上的单调递增.(8分)(本次未扣分,以后考试一定会扣分)
证明:设x1,x2为(-∞,+∞)上任意两个实数,且x1<x2,
则由a>1得

∴当a>1时,f(x)在(-∞,+∞)上的单调递增.(14分)
分析:(1)用奇偶性定义判断,先看f(x)的定义域是否关于原点对称,再看f(x)与f(-x)的关系.
(2)用单调性定义判断,思路是在区间上任取两个变量,且界定大小,再作差变形看符号.
点评:本题主要考查函数的奇偶性和单调性的判断.
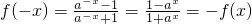 ,得∴f(x)为R上的奇函数.(6分)
,得∴f(x)为R上的奇函数.(6分)(2)当a>1时,f(x)在(-∞,+∞)上的单调递增.(8分)(本次未扣分,以后考试一定会扣分)
证明:设x1,x2为(-∞,+∞)上任意两个实数,且x1<x2,
则由a>1得


∴当a>1时,f(x)在(-∞,+∞)上的单调递增.(14分)
分析:(1)用奇偶性定义判断,先看f(x)的定义域是否关于原点对称,再看f(x)与f(-x)的关系.
(2)用单调性定义判断,思路是在区间上任取两个变量,且界定大小,再作差变形看符号.
点评:本题主要考查函数的奇偶性和单调性的判断.

练习册系列答案
相关题目
 ,则称f(x)是满足“倒负”变换的函数.下列四个函数:
,则称f(x)是满足“倒负”变换的函数.下列四个函数: ;
;  .
.