题目内容
f（x）=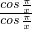
的不连续点为
- A.x=0
- B.x=
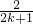（k=0，±1，±2，…） - C.x=0和x=2kπ（k=0，±1，±2，…）
- D.x=0和x=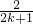（k=0，±1，±2，…）
D
分析：本题直接根据变化率与导数的基本概念，分析式子即可．
解答：由cos
=0，得=kπ+
（k∈Z），∴x=
．又x=0也不是连续点，故选D．
点评：本题考查变化率与导数的基本概念，分析好题中式子即可．
分析：本题直接根据变化率与导数的基本概念，分析式子即可．
解答：由cos
=0，得=kπ+（k∈Z），∴x=．又x=0也不是连续点，故选D．点评：本题考查变化率与导数的基本概念，分析好题中式子即可．
练习册系列答案
相关题目
下列四个命题中，不正确的是（ ）
A、若函数f（x）在x=x0处连续，则
| ||||||||
B、函数f(x)=
| ||||||||
C、若函数f（x）、g（x）满足
| ||||||||
D、
|
f（x）=
的不连续点为（ ）
cos
| ||
cos
|
| A、x=0 | ||
B、x=
| ||
| C、x=0和x=2kπ（k=0，±1，±2，…） | ||
D、x=0和x=
|