题目内容
已知直线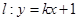 过定点
过定点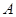 ,动点
,动点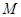 满足
满足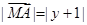 ,动点
,动点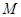 的轨迹为
的轨迹为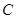 .
.
(Ⅰ)求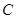 的方程;
的方程;
(Ⅱ)直线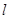 与
与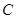 交于
交于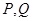 两点,以
两点,以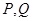 为切点分别作
为切点分别作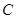 的切线,两切线交于点
的切线,两切线交于点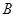 .
.
①求证: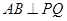 ;②若直线
;②若直线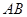 与
与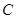 交于
交于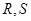 两点,求四边形
两点,求四边形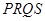 面积的最大值.
面积的最大值.
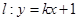 过定点
过定点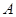 ,动点
,动点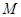 满足
满足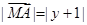 ,动点
,动点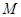 的轨迹为
的轨迹为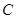 .
.(Ⅰ)求
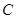 的方程;
的方程;(Ⅱ)直线
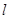 与
与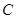 交于
交于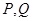 两点,以
两点,以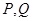 为切点分别作
为切点分别作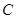 的切线,两切线交于点
的切线,两切线交于点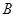 .
.①求证:
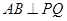 ;②若直线
;②若直线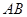 与
与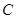 交于
交于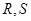 两点,求四边形
两点,求四边形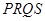 面积的最大值.
面积的最大值.(1)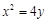 (2) 根据直线斜率互为负倒数来得到证明,当且仅当
(2) 根据直线斜率互为负倒数来得到证明,当且仅当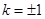 时,四边形
时,四边形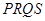 面积的取到最小值
面积的取到最小值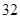 。
。
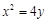 (2) 根据直线斜率互为负倒数来得到证明,当且仅当
(2) 根据直线斜率互为负倒数来得到证明,当且仅当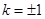 时,四边形
时,四边形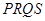 面积的取到最小值
面积的取到最小值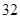 。
。试题分析:(I)由题意知
 ,设
,设
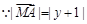
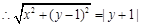 化简得
化简得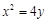 3分
3分(Ⅱ)①设
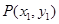 ,
,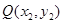 ,
,由
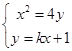 消去
消去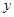 ,得
,得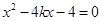 ,显然
,显然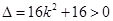 .
.所以
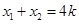 ,
,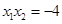
由
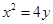 ,得
,得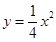 ,所以
,所以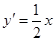 ,
, 所以,以
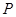 为切点的切线的斜率为
为切点的切线的斜率为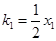 ,
,所以,以
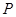 为切点的切线方程为
为切点的切线方程为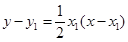 ,又
,又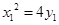 ,
,所以,以
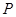 为切点的切线方程为
为切点的切线方程为 ……(1)
……(1)同理,以
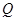 为切点的切线方程为
为切点的切线方程为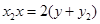 ……(2)
……(2)(2)-(1)并据
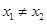 得点
得点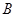 的横坐标
的横坐标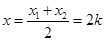 ,
,代入(1)易得点
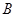 的纵坐标
的纵坐标 ,所以点
,所以点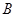 的坐标为
的坐标为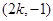
当
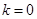 时,显然
时,显然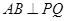
当
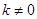 时,
时,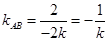 ,从而
,从而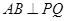 8分
8分②由已知,显然直线
 的斜率不为0,由①知
的斜率不为0,由①知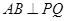 ,所以
,所以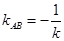 ,
,则直线
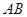 的方程为
的方程为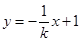 ,
,设设
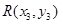 ,
,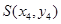 ,
,由
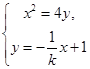 消去
消去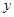 ,得
,得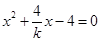 ,显然
,显然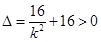 ,
,所以
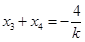 ,
, .
. 又
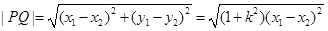
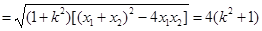
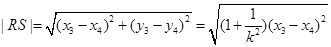
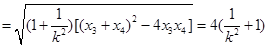
因为
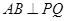 ,所以
,所以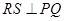 ,
, 所以,
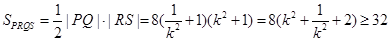 ,
,当且仅当
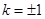 时,四边形
时,四边形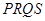 面积的取到最小值
面积的取到最小值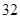 13分
13分点评:解决的关键是借助于向量的模来表示得到轨迹方程,并联立方程组来得到弦长公式,进而得到面积的表示,属于中档题。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
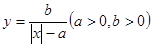 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与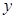 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当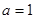 ,
,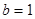 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .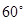 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若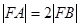 ,则椭圆的离心率为( )
,则椭圆的离心率为( )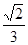 B.
B. 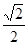 C.
C. 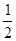 D.
D. 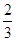
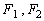 为双曲线
为双曲线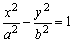 的左右焦点,点P在双曲线上,
的左右焦点,点P在双曲线上, 的平分线分线段
的平分线分线段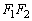 的比为5∶1,则双曲线的离心率的取值范围是 .
的比为5∶1,则双曲线的离心率的取值范围是 .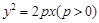 的焦点为
的焦点为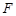 ,点
,点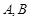 在此抛物线上,且
在此抛物线上,且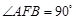 ,弦
,弦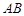 的中点
的中点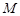 在该抛物线准线上的射影为
在该抛物线准线上的射影为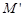 ,则
,则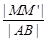 的最大值为( )
的最大值为( )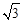
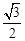
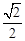
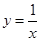 的图象为双曲线,在双曲线的两支上分别取点
的图象为双曲线,在双曲线的两支上分别取点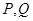 ,则线段
,则线段 的最小值为 ;
的最小值为 ; 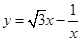 的图象为双曲线,在此双曲线的两支上分别取点
的图象为双曲线,在此双曲线的两支上分别取点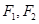 的椭圆
的椭圆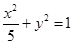 和双曲线
和双曲线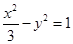 ,
,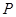 是它们的一个交点,则
是它们的一个交点,则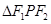 的形状是 ( )
的形状是 ( )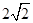 ,一个焦点的坐标为(1,0).
,一个焦点的坐标为(1,0).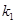 ,
,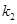 ,求证:
,求证: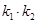 为定值.
为定值.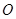 为原点,
为原点,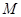 为动点,
为动点,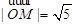 ,
,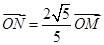 . 过点
. 过点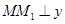 轴于
轴于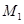 ,过
,过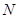 作
作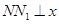 轴于点
轴于点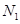 ,
,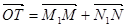 . 记点
. 记点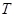 的轨迹为曲线
的轨迹为曲线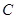 ,
,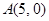 、
、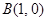 ,过点
,过点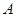 作直线
作直线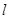 交曲线
交曲线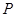 、
、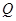 (点
(点 ,并说明理由.
,并说明理由.