Question

已知函数f(x)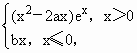＝g(x)＝clnx＋b，且x＝是函数y＝f(x)的极值点．

(Ⅰ)求实数a的值；

(Ⅱ)若方程f(x)－m＝0有两个不相等的实数根，求实数m的取值范围；

(Ⅲ)若直线l是函数y＝f(x)的图象在点(2，f(2))处的切线，且直线l与函数y＝g(x)的图象相切于点P(x₀，y₀)，x₀∈[e^－1，e]，求实数b的取值范围．

Answer 1

答案：
解析：

解析：(Ⅰ) 　　　2分 　　由已知， 　　 　　得a＝1　3分 　　(Ⅱ)由(Ⅰ) 　　 　　令　4分 　　当时 　　所以，当时，单调递减， 　　当 　　　5分 　　要使方程有两不相等的实数根，即函数的图象与直线有两个不同的交点． 　　(1)当时，m＝0或　6分 　　(2)当b＝0时，　7分 　　(3)当　8分 　　(Ⅲ)时， 　　 　　函数的图角在点处的切线的方程为：9分 　　直线与函数的图象相切于点， 　　，所以切线的斜率为 　　所以切线的方程为 　　即的方程为：　10分 　　得 　　得其中　11分 　　记其中 　　　12分 　　令 　　又 　　　13分 　　 　　所以实数b的取值范围的集合：　14分