Question

如图,在直三棱柱ABC—A₁B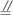₁C₁中,AB=BC,D、E分别为BB₁、AC₁的中点.

(1)证明ED为异面直线BB₁与AC₁的公垂线;

(2)设AA₁=AC=AB,求二面角A₁-AD-C₁的平面角大小.

Answer 1

(1)证明:设O为AC中点,连结EO、BO,则EOC₁C,又C₁CB₁B,

∴EODB,四边形EOBD为平行四边形,ED∥OB.

∵AB=BC,

∴BO⊥AC.

又平面ABC⊥平面ACC₁A₁,

BO面ABC,

故BO⊥平面ACC₁A₁,

∴ED⊥平面ACC₁A₁.

∴ED⊥AC₁,

ED⊥CC₁.

∴ED⊥BB₁.

∴ED为异面直线AC₁与BB₁的公垂线.

(2)解析:连结A₁E.由AA₁=AC=AB可知,四边形A₁ACC₁为正方形,

∴A₁E⊥AC₁.

又由ED⊥平面A₁ACC₁和ED平面ADC₁知平面ADC₁⊥平面A₁ACC₁,

∴A₁E⊥平面ADC₁.

作EF⊥AD,垂足为F,连结A₁F,则A₁F⊥AD,∠A₁FE为二面角A₁-AD-C₁的平面角.

不妨设AA₁=2,

则AC=2,AB=.

ED=OB=1,EF=,

tan∠A₁FE=.

∴∠A₁FE=60°.

∴二面角A₁-AD-C₁的平面角为60°.