Question

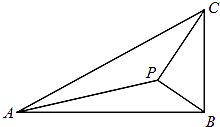如图，在△ABC中，∠ABC=90°，AB=

3

，BC=1，P为△ABC内一点，∠BPC=90°
（Ⅰ）若PB=

1

2

，求PA；
（Ⅱ）若∠APB=150°，求tan∠PBA．

Answer 1

分析：（I）在Rt△PBC，利用边角关系即可得到∠PBC=60°，得到∠PBA=30°．在△PBA中，利用余弦定理即可求得PA．
（II）设∠PBA=α，在Rt△PBC中，可得PB=sinα．在△PBA中，由正弦定理得

AB

sin∠APB

=

PB

sin∠PAB

，即

3

sin150°

=

sinα

sin(30°-α)

，化简即可求出．

解答：解：（I）在Rt△PBC中，cos∠PBC=

PB

BC

=

1

2

，∴∠PBC=60°，∴∠PBA=30°．
在△PBA中，由余弦定理得PA²=PB²+AB²-2PB•ABcos30°=(

1

2

)2+(

3

)2-2×

1

2

×

3

×

3

2

=

7

4

．
∴PA=

7

2

．
（II）设∠PBA=α，在Rt△PBC中，PB=BCcos（90°-α）=sinα．
在△PBA中，由正弦定理得

AB

sin∠APB

=

PB

sin∠PAB

，即

3

sin150°

=

sinα

sin(30°-α)

，
化为

3

cosα=4sinα．∴tanα=

3

4

．

点评：熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键．