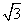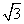题目内容
设双曲线 x2-m y2=1离心率不小于| 3 |
分析:先双曲线 x2-m y2=1化成标准方程得:
-
=1得出a2=1,b2=
,根据由离心率不小于
得得出m的取值范围,结合点到直线的距离,从而得出此双曲线焦点到渐近线的最小距离.
| x2 |
| 1 |
| y2 | ||
|
| 1 |
| m |
| 3 |
解答:解:双曲线 x2-m y2=1化成标准方程得:
-
=1
a2=1,b2=
,
∴c2=1+
,由离心率不小于
得:
1+
≥(
)2
∴m≤
,
∴双曲线焦点到渐近线的距离为:d=
=
≤
此双曲线焦点到渐近线的最小距离为
,
故答案为:
| x2 |
| 1 |
| y2 | ||
|
a2=1,b2=
| 1 |
| m |
∴c2=1+
| 1 |
| m |
| 3 |
1+
| 1 |
| m |
| 3 |
∴m≤
| 1 |
| 2 |
∴双曲线焦点到渐近线的距离为:d=
|
| ||||
|
| 1 | ||
|
| 2 |
此双曲线焦点到渐近线的最小距离为
| 2 |
故答案为:
| 2 |
点评:本小题主要考查双曲线的简单性质、点到直线的距离等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
相关题目
 ,此双曲线焦点到渐近线的最小距离为________.
,此双曲线焦点到渐近线的最小距离为________.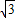 ,此双曲线焦点到渐近线的最小距离为 .
,此双曲线焦点到渐近线的最小距离为 .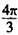 ,则实数m的值为
,则实数m的值为