题目内容
在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.
(1)若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.
(1)由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从袋中10个球中摸出2个,试验的结果共有
=45(种).
满足条件的中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为
=15;
(ii)2个球都是白色,包含的基本事件数为
=6.
∴中奖这个事件包含的基本事件数为15+6=21.
∴中奖概率为
=
.
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.
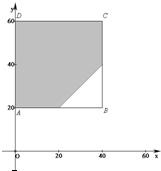
用(x,y)表示每次试验的结果,则所有可能结果为Ω={(x,y)|0≤x≤40,20≤y≤60};
记甲比乙提前到达为事件A,则事件A的可能结果为A={(x,y)|x<y,0≤x≤40,20≤y≤60}.
如图所示,试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.
根据几何概型公式,得到P(A)=
=
=
.
∴甲比乙提前到达的概率为
.
试验发生包含的事件是从袋中10个球中摸出2个,试验的结果共有
| 10×9 |
| 2 |
满足条件的中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为
| 6×5 |
| 2 |
(ii)2个球都是白色,包含的基本事件数为
| 4×3 |
| 2 |
∴中奖这个事件包含的基本事件数为15+6=21.
∴中奖概率为
| 21 |
| 45 |
| 7 |
| 15 |
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.
用(x,y)表示每次试验的结果,则所有可能结果为Ω={(x,y)|0≤x≤40,20≤y≤60};
记甲比乙提前到达为事件A,则事件A的可能结果为A={(x,y)|x<y,0≤x≤40,20≤y≤60}.
如图所示,试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.
根据几何概型公式,得到P(A)=
| S阴影 |
| S正方形 |
402-
| ||
| 402 |
| 7 |
| 8 |
∴甲比乙提前到达的概率为
| 7 |
| 8 |


练习册系列答案
相关题目