Question

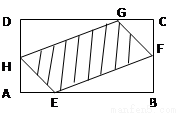
（本题满分10分） 如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB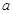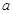＝（>2），BC＝2，且AE＝AH＝CF＝CG，

设AE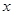＝，绿地面积为.

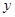（1）写出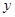关于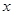的函数关系式，并指出这个函数的定义域;

（2）当AE为何值时，绿地面积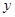最大？

 

Answer 1

【答案】

（1）S_ΔAEH＝S_ΔCFG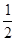＝x²， S_ΔBEF＝S_ΔDGH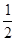＝（－x）（2－x）

∴y＝S_ABCD－2S_ΔAEH－2S_ΔBEF＝2－x²－（－x）（2－x）＝－2x²＋（＋2）x

∴y＝－2x²＋（＋2）x，0<x≤2

（2）当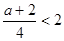，即<6时，则x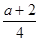＝时，y取最大值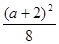

当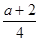≥2，即≥6时，y＝－2x²＋（＋2）x，在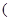0，2]上是增函数，

  则x＝2时，y取最大值2－4

综上所述：当<6时，AE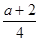＝时，绿地面积取最大值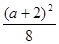

当≥6时，AE＝2时，绿地面积取最大值2－4

【解析】本题主要考查实际问题中的建模和解模能力，注意二次函数求最值的方法．

（1）先求得四边形ABCD，△AHE的面积，再分割法求得四边形EFGH的面积，即建立y关于x的函数关系式；

（2）由（1）知y是关于x的二次函数，用二次函数求最值的方法求解．

（1）S_ΔAEH＝S_ΔCFG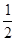＝x²， S_ΔBEF＝S_ΔDGH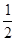＝（－x）（2－x）

∴y＝S_ABCD－2S_ΔAEH－2S_ΔBEF＝2－x²－（－x）（2－x）＝－2x²＋（＋2）x

∴y＝－2x²＋（＋2）x，0<x≤2

（2）当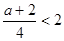，即<6时，则x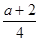＝时，y取最大值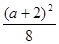

当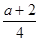≥2，即≥6时，y＝－2x²＋（＋2）x，在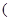0，2]上是增函数，

  则x＝2时，y取最大值2－4

综上所述：当<6时，AE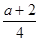＝时，绿地面积取最大值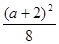

当≥6时，AE＝2时，绿地面积取最大值2－4