题目内容
5.在正四棱锥S-ABCD中,SA=2$\sqrt{3}$,当该棱锥的体积最大时,它的外接球(正四棱锥的顶点都在球的表面上)的体积为36π.分析 设出底面边长,求出正四棱锥的高,写出体积表达式,利用求导求得最大值时,高的值,再求出外接球的半径,即可得出结论.
解答 解:设底面边长为a,则高h=$\sqrt{12-\frac{{a}^{2}}{2}}$,
所以体积V=$\frac{1}{3}$a2h=$\frac{1}{3}\sqrt{12{a}^{4}-\frac{1}{2}{a}^{6}}$,
设y=12a4-$\frac{1}{2}$a6,则y′=48a3-3a5,当y取最值时,y′=48a3-3a5=0,解得a=0或a=4时,
当a=4时,体积最大,此时h=2,
设外接球的半径为R,则R2=(2-R)2+(2$\sqrt{2}$)2,
所以R=3,
所以外接球(正四棱锥的顶点都在球的表面上)的体积为$\frac{4}{3}π•{3}^{3}$=36π.
故答案为:36π.
点评 本试题主要考查锥体的体积,考查高次函数的最值问题的求法.是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
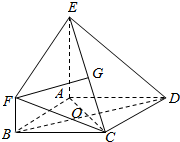 在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O
在如图所示的几何体中,底面ABCD是边长为2的菱形,∠ABC=60°,EA⊥平面ABCD,EA∥BF,EA=2BF=2,G为CE的中点,直线AC与BD相交于点O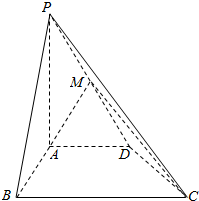 如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.