题目内容
已知向 a=(x,2),
a=(x,2), =(1,y),其中x>0,y>0.若
=(1,y),其中x>0,y>0.若 •
• =4,则
=4,则 的最小值为
的最小值为
- A.

- B.2
- C.

- D.2

C
分析:由向量数量积坐标运算公式,得x+2y=4,从而得到 =
= (x+2y)(
(x+2y)( ),展开后再用基本不等式,即可得到所要求的最小值.
),展开后再用基本不等式,即可得到所要求的最小值.
解答:∵向量 =(x,2),
=(x,2), =(1,y),
=(1,y),
∴ •
• =x+2y=4,得
=x+2y=4,得 (x+2y)=1
(x+2y)=1
由此可得 =
= (x+2y)(
(x+2y)( )=
)= (5+
(5+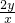 +
+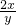 )
)
∵x>0,y>0.
∴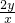 +
+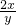 ≥2
≥2 =4,可得
=4,可得 ≥
≥ ×9=
×9=
当且仅当x=y= 时,
时, 的最小值为
的最小值为
故选:C
点评:本题已知向量数量积,求关于x、y分式的最值,着重考查了平面向量及应用和用基本不等式求最值等知识,属于基础题.
分析:由向量数量积坐标运算公式,得x+2y=4,从而得到
 =
= (x+2y)(
(x+2y)( ),展开后再用基本不等式,即可得到所要求的最小值.
),展开后再用基本不等式,即可得到所要求的最小值.解答:∵向量
 =(x,2),
=(x,2), =(1,y),
=(1,y),∴
 •
• =x+2y=4,得
=x+2y=4,得 (x+2y)=1
(x+2y)=1由此可得
 =
= (x+2y)(
(x+2y)( )=
)= (5+
(5+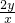 +
+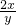 )
)∵x>0,y>0.
∴
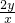 +
+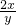 ≥2
≥2 =4,可得
=4,可得 ≥
≥ ×9=
×9=
当且仅当x=y=
 时,
时, 的最小值为
的最小值为
故选:C
点评:本题已知向量数量积,求关于x、y分式的最值,着重考查了平面向量及应用和用基本不等式求最值等知识,属于基础题.

练习册系列答案
相关题目
 a=(x,2),
a=(x,2), =(1,y),其中x>0,y>0.若
=(1,y),其中x>0,y>0.若 •
• =4,则
=4,则 的最小值为( )
的最小值为( )

