题目内容
在正三棱柱ABC-A1B1C1中,已知AB=1,点D在棱BB1上,且BD=1,则AD与平面AA1CC1所成角的正切值为
- A.

- B.1
- C.
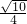
- D.

D
分析:根据题意画出图形,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,证明DG⊥面AA1C1C,∠DAG=α,解直角三角形ADG即可.
解答: 解:如图所示,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,
解:如图所示,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,
在正三棱柱中,有B1E⊥面AA1C1C,BF⊥面AA1C1C,
故DG⊥面AA1C1C,
∴∠DAG=α,可求得DG=BF= ,
,
AG= ,
,
故tanα=
故选D.
点评:考查直线和平面所成的角,关键是找到斜线在平面内的射影,把空间角转化为平面角求解,属基础题.
分析:根据题意画出图形,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,证明DG⊥面AA1C1C,∠DAG=α,解直角三角形ADG即可.
解答:
 解:如图所示,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,
解:如图所示,过B作BF⊥AC,过B1作B1E⊥A1C1,连接EF,过D作DG⊥EF,连接AG,在正三棱柱中,有B1E⊥面AA1C1C,BF⊥面AA1C1C,
故DG⊥面AA1C1C,
∴∠DAG=α,可求得DG=BF=
 ,
,AG=
 ,
,故tanα=

故选D.
点评:考查直线和平面所成的角,关键是找到斜线在平面内的射影,把空间角转化为平面角求解,属基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.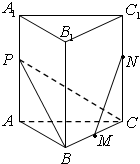 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为