题目内容
计算∫02|1-x2|dx=分析：先根据定积分的几何意义，将原式化成：∫01（1-x2）dx+∫12（x2-1）dx，再利用定积分的运算法则，找出被积函数的原函数，进行计算即可．
解答：
解：原式
=∫01（1-x2）dx+∫12（x2-1）dx
=（x-
x3）|01+（
x3-x）|12
=
+
=2．
故答案为：2．
解：原式=∫01（1-x2）dx+∫12（x2-1）dx
=（x-
| 1 |
| 3 |
| 1 |
| 3 |
=
| 2 |
| 3 |
| 4 |
| 3 |
=2．
故答案为：2．
点评：本题主要考查定积分的基本运算，解题关键是找出被积函数的原函数，利用区间去绝对值符号也是注意点，本题属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
某校高二年级兴趣小组，为了分析2011年我国宏观经济形势，上网查阅了2010年和2011年1-10月我国GPI同比（即当年某月与前一年同月相比）的增长数据（见下表），但今年4，5两个月的数据（分别记为x，y）没有查到．有的同学清楚记得今年3，4，5三个月的GPI数据的平均数是5.4，方差的3倍是0.02，且x＜y．
附表：我国2010年和2011年前十月的GPI数据（单位：百分点）
注：1个百分点=1%
（1）求x，y的值；
（2）一般认为，某月GPI达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点则严重通货膨胀．现随机地从2010年的十个月和2011年的十个月的数据中各抽取一个数据，求相同月份2010年通货膨胀，并且2011年严重通货膨胀的概率．
注：方差计算公式：s2=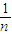
[（x1-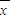
）2+（x2-
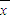）2+L+（xn-
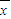）2）]，其中：
．
附表：我国2010年和2011年前十月的GPI数据（单位：百分点）
| 年份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 | 九月 | 十月 |
| 2010 | 1.5 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 | 3.3 | 3.5 | 3.6 | 4.4 |
| 2011 | 4.9 | 4.9 | 5.4 | x | y | 6.4 | 6.5 | 6.2 | 6.1 | 5.5 |
（1）求x，y的值；
（2）一般认为，某月GPI达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点则严重通货膨胀．现随机地从2010年的十个月和2011年的十个月的数据中各抽取一个数据，求相同月份2010年通货膨胀，并且2011年严重通货膨胀的概率．
注：方差计算公式：s2=
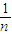[（x1-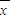）2+（x2-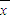）2+L+（xn-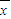）2）]，其中：．