题目内容
已知M={x | x2-2x-3=0},N={x | x2+ax+1=0,a∈R},且N![]() M,求a 的取值范围、
M,求a 的取值范围、
解:M={x | x2-2x-3=0}={3,-1}
∵N![]() M
M
当N= ![]() 时,N
时,N![]() M 成立
M 成立
N={x | x2+ax+1=0}
∴a2-4<0
∴-2<a<2
当N≠![]() 时,∵N
时,∵N![]() M
M
∴3∈N或 -1∈N
当3∈N时,32-3a+1=0即a= -![]() ,N={3,
,N={3,![]() }不满足N
}不满足N![]() M
M
当-1∈N时,(-1)2-a+1=0即a=2,N={-1} 满足N![]() M
M
∴ a的取値范围是:-2<x≤2

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知M={x|y=
},N={y|y=x2+2x+1},则M∩N=( )
| x2-1 |
| A、{x|x≥0} |
| B、{x|x≤-1} |
| C、{x|x≥1} |
| D、φ |
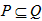 ,求实数a的取值范围.
,求实数a的取值范围.