题目内容
数列{an}中,a1=1,a2=r>0,数列{anan+1}为公比为q(q>0)的等比数列,数列{bn}中,bn=a2n—1+a2n.
(1)求使anan+1+an+1an+2>an+2an+3成立的公比q的取值范围;
(2)求{bn}的通项
(3)若r=219. 2 -1,q=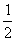 ,求数列{
,求数列{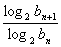 }的最大项和最小项.
}的最大项和最小项.
(1)1+q>q2,∴q∈( ,0)∪(0,
,0)∪(0, ). 又q>0 ∴q∈(0,
). 又q>0 ∴q∈(0, )
)
(2)q= =
= ,说明{an}的奇数项构成首项为1,公比为q的等比数列,偶数项构成首项r,公比q的等比数列,bn=a2n—1+a2n=(1+r)qn—1.
,说明{an}的奇数项构成首项为1,公比为q的等比数列,偶数项构成首项r,公比q的等比数列,bn=a2n—1+a2n=(1+r)qn—1.
(3 )由已知,
)由已知, ,log2bn=20.2-n,故{
,log2bn=20.2-n,故{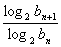 }的通项(第n项为)为
}的通项(第n项为)为 ,
,
当n=20时为负值-4 ,在[1,19]单调递减且小于1,故n=21时当最大项是
,在[1,19]单调递减且小于1,故n=21时当最大项是

练习册系列答案
相关题目
 的无穷等比数列
的无穷等比数列
 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列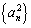 各项的和为
各项的和为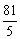 .
.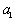 和公比
和公比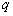 ;
;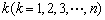 ,设
,设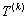 是首项为
是首项为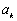 ,公差为
,公差为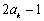 的等差数列,求
的等差数列,求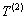 的前10项之和;
的前10项之和;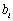 为数列
为数列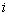 项,
项,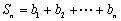 ,求
,求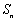 ,并求正整数
,并求正整数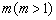 ,使得
,使得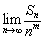 存在且不等于零.
存在且不等于零.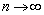 时该无穷等比数列前
时该无穷等比数列前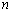 项和的极限)
项和的极限) 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,则
,则 ( )
( ) C.10 D.9
C.10 D.9 ,若对任意
,若对任意 有
有 成立,则方程
成立,则方程 在
在 上的解为__________
上的解为__________ ,则( C )
,则( C ) A.
A. B.
B.
 D.前三个判断都不
D.前三个判断都不 正确
正确 则
则 的最小值为
的最小值为 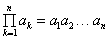 ,
,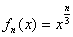 ,
,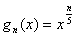 ,
,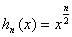 ,
,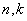 为正整数.给
为正整数.给 出下列三个论断:
出下列三个论断: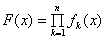 是偶函数的最小正整数
是偶函数的最小正整数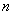 的值等于3;
的值等于3;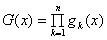 是偶函数的最小正整数
是偶函数的最小正整数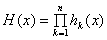 是奇
是奇 函数的最小正整数
函数的最小正整数 <1的解集为(-∞ ,1)∪(2,+∞),则a=_____
<1的解集为(-∞ ,1)∪(2,+∞),则a=_____ 满足
满足 则____________
则____________