题目内容
若双曲线 -
- =1的渐近线与抛物线y2=2px(p>0)的准线相交于A,B两点,且△OAB(O为原点)为等边三角形,则p的值为 .
=1的渐近线与抛物线y2=2px(p>0)的准线相交于A,B两点,且△OAB(O为原点)为等边三角形,则p的值为 .
【答案】分析:求出双曲线 -
- =1的渐近线方程与抛物线y2=2px(p>0)的准线方程,进而求出A,B两点的坐标,再由△OAB(O为原点)为等边三角形,可得出点A,B到x轴的距离恰为原点到抛物线的准线距离的
=1的渐近线方程与抛物线y2=2px(p>0)的准线方程,进而求出A,B两点的坐标,再由△OAB(O为原点)为等边三角形,可得出点A,B到x轴的距离恰为原点到抛物线的准线距离的 倍,由此方程求出p的值
倍,由此方程求出p的值
解答:解:∵双曲线 -
- =1
=1
∴综的渐近线方程是y=±
又抛物线y2=2px(p>0)的准线方程是x=-
故A,B两点的纵坐标分别是y=±
又△OAB(O为原点)为等边三角形,x轴是角AOB的角平分线
∴ ×
× =
= ,得p=4
,得p=4
故答案为4
点评:本题考查圆锥曲线的共同特征,解题的关键是求出双曲线的渐近线方程,解出A,B两点的坐标,再由△OAB(O为原点)为等边三角形建立关于参数的方程求参数,本题有一定的运算量,做题时要严谨,防运算出错
 -
- =1的渐近线方程与抛物线y2=2px(p>0)的准线方程,进而求出A,B两点的坐标,再由△OAB(O为原点)为等边三角形,可得出点A,B到x轴的距离恰为原点到抛物线的准线距离的
=1的渐近线方程与抛物线y2=2px(p>0)的准线方程,进而求出A,B两点的坐标,再由△OAB(O为原点)为等边三角形,可得出点A,B到x轴的距离恰为原点到抛物线的准线距离的 倍,由此方程求出p的值
倍,由此方程求出p的值解答:解:∵双曲线
 -
- =1
=1∴综的渐近线方程是y=±

又抛物线y2=2px(p>0)的准线方程是x=-

故A,B两点的纵坐标分别是y=±

又△OAB(O为原点)为等边三角形,x轴是角AOB的角平分线
∴
 ×
× =
= ,得p=4
,得p=4故答案为4
点评:本题考查圆锥曲线的共同特征,解题的关键是求出双曲线的渐近线方程,解出A,B两点的坐标,再由△OAB(O为原点)为等边三角形建立关于参数的方程求参数,本题有一定的运算量,做题时要严谨,防运算出错

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 -
- =1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )
=1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )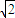
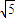

 -
- =1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )
=1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )

