题目内容
当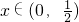 时,函数y=loga(-x2+logax)有意义,则实数a∈________.
时,函数y=loga(-x2+logax)有意义,则实数a∈________.
[ ,1)
,1)
分析:由题意,-x2+logax>0在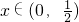 上恒成立,即logax>x2恒成立,可结合函数的图象求解.
上恒成立,即logax>x2恒成立,可结合函数的图象求解.
解答: 解:由题意,-x2+logax>0在
解:由题意,-x2+logax>0在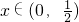 上恒成立,即logax>x2恒成立,如图:
上恒成立,即logax>x2恒成立,如图:
当a>1时不符合要求;
当0<a<1时,若y=logax过点( ,
, ),即
),即 ,所以a=
,所以a= ,故
,故 ≤a<1,
≤a<1,
综上所述,a的范围为:[ ,1)
,1)
点评:本题考查对数函数的定义域、不等式恒成立问题,考查转化思想和数形结合思想.
 ,1)
,1)分析:由题意,-x2+logax>0在
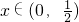 上恒成立,即logax>x2恒成立,可结合函数的图象求解.
上恒成立,即logax>x2恒成立,可结合函数的图象求解.解答:
 解:由题意,-x2+logax>0在
解:由题意,-x2+logax>0在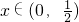 上恒成立,即logax>x2恒成立,如图:
上恒成立,即logax>x2恒成立,如图:当a>1时不符合要求;
当0<a<1时,若y=logax过点(
 ,
, ),即
),即 ,所以a=
,所以a= ,故
,故 ≤a<1,
≤a<1,综上所述,a的范围为:[
 ,1)
,1)点评:本题考查对数函数的定义域、不等式恒成立问题,考查转化思想和数形结合思想.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 时,求函数的值域.
时,求函数的值域.