题目内容
如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数
 的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.(1)求f(t)的解析式;
(2)求面积S=f(t)的最大值.

【答案】分析:(1)求出函数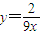 的导函数,写出经过P(t,
的导函数,写出经过P(t,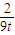 )的切线方程并得到切线在两坐标轴上的截距,然后根据两截距与1的关系对t分类,求出t在不同范围内的切线左下方的面积,则分段函数的解析式可求;
)的切线方程并得到切线在两坐标轴上的截距,然后根据两截距与1的关系对t分类,求出t在不同范围内的切线左下方的面积,则分段函数的解析式可求;
(2)直接利用二次函数的单调性求各区间段内函数的最值,然后各段内最大值的最大者.
解答:解:(1)因为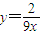 ,所以
,所以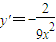 ,又P(t,
,又P(t,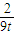 ),
),
所以过点P的切线方程为 ,即
,即 ,
,
令x=0,得 ,令y=0,得x=2t.
,令y=0,得x=2t.
所以切线与x轴交点E(2t,0),切线与y轴交点 .
.
①当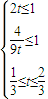 ,即
,即 时,切线左下方的区域为一直角三角形,
时,切线左下方的区域为一直角三角形,
所以 ;
;
②当 ,即
,即 时,切线左下方的区域为一直角梯形,
时,切线左下方的区域为一直角梯形,
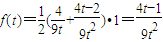 ;
;
③当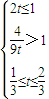 ,即
,即 时,切线左下方的区域为一直角梯形,
时,切线左下方的区域为一直角梯形,
所以 .
.
综上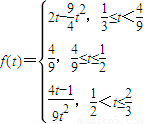 .
.
(2)当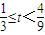 时,
时, =
=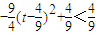 ,
,
当 时,
时,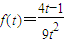 =
= ,
,
所以 .
.
所以面积S=f(t)的最大值为 .
.
点评:本题考查了函数模型的选择与应用,考查了分类讨论的数学思想方法,训练了利用二次函数的单调性求函数的最值,需要注意的是分段函数的最值要分段求,属中档题.
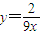 的导函数,写出经过P(t,
的导函数,写出经过P(t,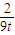 )的切线方程并得到切线在两坐标轴上的截距,然后根据两截距与1的关系对t分类,求出t在不同范围内的切线左下方的面积,则分段函数的解析式可求;
)的切线方程并得到切线在两坐标轴上的截距,然后根据两截距与1的关系对t分类,求出t在不同范围内的切线左下方的面积,则分段函数的解析式可求;(2)直接利用二次函数的单调性求各区间段内函数的最值,然后各段内最大值的最大者.
解答:解:(1)因为
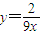 ,所以
,所以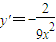 ,又P(t,
,又P(t,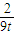 ),
),所以过点P的切线方程为
 ,即
,即 ,
,令x=0,得
 ,令y=0,得x=2t.
,令y=0,得x=2t.所以切线与x轴交点E(2t,0),切线与y轴交点
 .
.①当
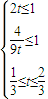 ,即
,即 时,切线左下方的区域为一直角三角形,
时,切线左下方的区域为一直角三角形,所以
 ;
;②当
 ,即
,即 时,切线左下方的区域为一直角梯形,
时,切线左下方的区域为一直角梯形,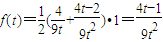 ;
;③当
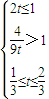 ,即
,即 时,切线左下方的区域为一直角梯形,
时,切线左下方的区域为一直角梯形,所以
 .
.综上
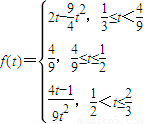 .
.(2)当
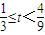 时,
时, =
=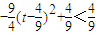 ,
,当
 时,
时,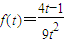 =
= ,
,所以
 .
.所以面积S=f(t)的最大值为
 .
.点评:本题考查了函数模型的选择与应用,考查了分类讨论的数学思想方法,训练了利用二次函数的单调性求函数的最值,需要注意的是分段函数的最值要分段求,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
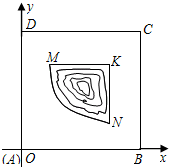 (2011•徐州模拟)如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数
(2011•徐州模拟)如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数 如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数
如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数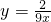
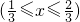 的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
 的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
的图象,另外的边缘是平行于正方形两边的直线段.为了美化该地块,计划修一条穿越该地块的直路(宽度不计),直路l与曲线段MN相切(切点记为P),并把该地块分为两部分.记点P到边AD距离为t,f(t)表示该地块在直路左下部分的面积.
 如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数
如图,某新建小区有一片边长为1(单位:百米)的正方形剩余地块ABCD,中间部分MNK是一片池塘,池塘的边缘曲线段MN为函数