题目内容
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
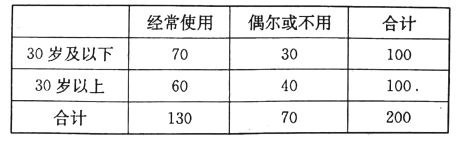
(Ⅰ)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
市使用共享单车情况与年龄有关?(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:

【答案】(1) 能在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关
市使用共享单车情况与年龄有关
(2) ![]()
![]()
【解析】试题分析:(1)根据公式得到![]() ,从而得到结果;(2)由条件得到
,从而得到结果;(2)由条件得到![]() ,根据二项分布的公式得到期望值。
,根据二项分布的公式得到期望值。
解析:
(Ⅰ)由列联表可知,
![]() .
.
∵![]() ,
,
∴能在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关.
市使用共享单车情况与年龄有关.
(Ⅱ)①依题意,可知所抽取的10名30岁以上网民中,经常使用共享单车的有![]() (人),
(人),
偶尔或不用共享单车的有![]() (人).
(人).
则选出的3人中至少2人经常使用共享单车的概率为![]() .
.
②由![]() 列联表,可知抽到经常使用共享单位的频率为
列联表,可知抽到经常使用共享单位的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,
市市民中任意抽取1人,
恰好抽到经常使用共享单车的市民的概率为![]() .
.
由题意得![]() ,∴
,∴ ![]() ;
; ![]() .
.

【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: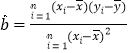 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.