题目内容
19.已知数列{an}满足a1=1,an+1=an2+an,用[x]表示不超过x的最大整数,则[$\frac{1}{{a}_{1}+1}$+$\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$]=0.分析 通过对an+1=an2+an两边同时取倒数、整理可知$\frac{1}{1+{a}_{n}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,并项相加得$\frac{1}{{a}_{1}+1}$+$\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$,利用an+1>an>1及取整函数即得结论.
解答 解:对an+1=an2+an两边同时取倒数,得:
$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}(1+{a}_{n})}$=$\frac{1}{{a}_{n}}$-$\frac{1}{1+{a}_{n}}$,
∴$\frac{1}{1+{a}_{n}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,
∴$\frac{1}{{a}_{1}+1}$+$\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$
=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{2015}}$-$\frac{1}{{a}_{2016}}$
=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$,
∵an+1=an2+an,a1=1,
∴an+1>an>1,
∴0<$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$<1,
∴[$\frac{1}{{a}_{1}+1}$+$\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$]=0,
故答案为:0.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | 6π cm | B. | 60 cm | C. | (40+6π) cm | D. | 1 080 cm |
| A. | 零向量是唯一没有方向的向量 | |
| B. | 平面内的单位向量有且仅有一个 | |
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$是共线向量,$\overrightarrow{b}$与$\overrightarrow{c}$是平行向量,则$\overrightarrow{a}$与$\overrightarrow{c}$是方向相同的向量 | |
| D. | 相等的向量必是共线向量 |
| A. | 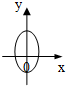 | B. | 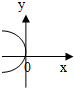 | C. | 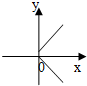 | D. | 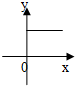 |
| A. | a2+a10>2a6 | B. | a2+a10<2a6 | ||
| C. | a2+a10=2a6 | D. | a2+a10与2a6的大小与a有关 |
| A. | 充分而不必要 | B. | 必要而不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
 如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$. 在长方体ABCD-A1B1C1D1中,E为DD1的中点.
在长方体ABCD-A1B1C1D1中,E为DD1的中点.