题目内容
已知 为常数,若曲线
为常数,若曲线 存在与直线
存在与直线 垂直的切线,则实数
垂直的切线,则实数 的取值范围是( )
的取值范围是( )
A、 B、
B、 C、
C、 D、
D、
【答案】
A
【解析】
试题分析:因为直线x+y-1=0直线的斜率为-1,那么所求的曲线的切线的斜率为1,故设切点为(m,n),则因为f’(x)=2ax+3- =1方程有解,同时要助于定义域x>0,那么分离参数2ax=
=1方程有解,同时要助于定义域x>0,那么分离参数2ax= -2,可得a=
-2,可得a= (x>0),求解右边函数的值域即为参数a的范围。则根据
(x>0),求解右边函数的值域即为参数a的范围。则根据 ,结合二次函数的性质可知其范围是a
,结合二次函数的性质可知其范围是a ,故选A.
,故选A.
考点:本题主要考查了导数的几何意义的运用。
点评:解决该试题的关键是利用两条直线的垂直关系,得到切线的斜率值,然后利用导数的几何意义,得到该点的导数值。进而方程有解得到a的范围。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
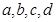 为常数,若不等式
为常数,若不等式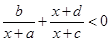 的解集为
的解集为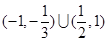 ,则不等式
,则不等式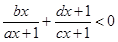 的解集为( )
的解集为( )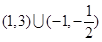 B.
B.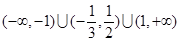
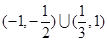 D.
D.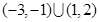
 为常数,若
为常数,若 ,
, ,则
,则 .
.