题目内容
已知有公共焦点的椭圆与双曲线中心在原点,焦点在x轴上,左右焦点分别为F1,F2,且它们在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,双曲线的离心率的值为2,则该椭圆的离心率的值为________.

分析:利用离心率的定义,及双曲线的离心率的值为2,|PF1|=10,|F1F2|=|PF2|,可求得|PF2|=
 ,再利用椭圆的离心率e2=
,再利用椭圆的离心率e2= ,可得结论.
,可得结论.解答:由题意知双曲线的离心率e1=
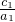 =
= =
= =2,
=2,又|PF1|=10,|F1F2|=|PF2|,
∴|PF2|=

∴椭圆的离心率e2=
 =
=
故答案为:

点评:本题考查椭圆与双曲线的几何性质,解题的关键是正确运用离心率的定义,属于中档题.

练习册系列答案
相关题目
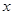 轴上,左右焦点分别为
轴上,左右焦点分别为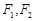 ,且它们在第一象限的交点为P,
,且它们在第一象限的交点为P,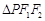 是以
是以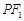 为底边的等腰三角形.若
为底边的等腰三角形.若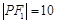 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为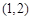 .则该椭圆的离心率的取值范围是
.则该椭圆的离心率的取值范围是