题目内容
求下列函数的反函数:(1)y=-![]() (-1≤x<0);
(-1≤x<0);
(2)y=-x2-2x+1(1≤x≤2);
(3)y=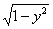
解:(1)由y=-![]() ,得y2=1-x2,
,得y2=1-x2,
即x2=1-y2.
∵-1≤x<0,
∴x=-![]() .
.
又∵y=-![]() ,-1≤x<0,
,-1≤x<0,
∴-1<y≤0.
∴所求反函数为y=-![]() (-1<x≤0).
(-1<x≤0).
(2)由y=-x2-2x+1=-(x+1)2+2,得(x+1)2=2-y.
∵1≤x≤2,
∴2≤x+1≤3.
∴x+1=![]() ,即x=-1+
,即x=-1+![]() .
.
∴反函数为y=-1+![]() (-7≤x≤-2).
(-7≤x≤-2).
(3)①由y=x2(x≤0),得x=-![]() ,即y=x2(x≤0)的反函数为y=-
,即y=x2(x≤0)的反函数为y=-![]() (x≥0).
(x≥0).
②由y=-x-1(x>0),得x=-y-1,即y=-x-1(x>0)的反函数为y=-x-1(x<-1).
由①②可知f(x)=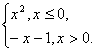 的反函数为f-1(x)=
的反函数为f-1(x)=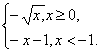

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 )x
)x