题目内容
设
>α>β>0，求证：α－β>sin α－sin β.
证明 如图所示，设单位圆与角α、β的终边分别交于P1、P2，作P1M1⊥x轴于M1，作P2M2⊥x轴于M2，作P2C⊥P1M1于C，连结P1P2，则sin α＝M1P1，sin β＝M2P2，α－β＝
，
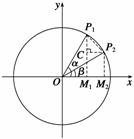
∴α－β＝>P1P2>CP1＝M1P1－M1C＝M1P1－M2P2＝sin α－sin β，即α－β>sin α－
sin β.
练习册系列答案
相关题目
题目内容
设>α>β>0，求证：α－β>sin α－sin β.
证明 如图所示，设单位圆与角α、β的终边分别交于P1、P2，作P1M1⊥x轴于M1，作P2M2⊥x轴于M2，作P2C⊥P1M1于C，连结P1P2，则sin α＝M1P1，sin β＝M2P2，α－β＝，
∴α－β＝>P1P2>CP1＝M1P1－M1C＝M1P1－M2P2＝sin α－sin β，即α－β>sin α－
sin β.
时f(x)是增函数，则f(-2),f(
),f(-3)的大小关系是：（ ） 
，其中x∈R，m是正整数，且
，这是组合数
（n、m是正整数，且m≤n）的一种推广．
的值；
取得最小值？
. ②
.
（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由.
”索的因应是( )
，函数f（x）的图像与x轴的交点也在函数g（x）的图像上，且在此点处f（x）与g（x）有公切线.