题目内容
的展开式中x2的系数是 ．
【答案】分析：根据题意，由二项式定理可得（1-x）4与（1-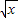
）3的展开式的通项，由因式乘法法则分析可得要使
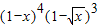的展开式中出现x2项，有2种情况，①（1-x）4中出x2项，（1-
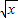）3中出常数项，②（1-x）4中出x项，（1-
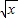）3中出x项即
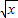的平方项，由二项式定理分别求出其系数，进而将其相加可得答案．
解答：解：根据题意，（1-x）4的展开式的通项为Tr+1=C4r（-x）r=（-1）rC4r xr，
（1-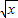
）3的展开式的通项为Tr+1=C3r（-
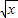）r=（-1）rC4r 
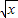r，
要使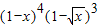
的展开式中出现x2项，有2种情况，
①（1-x）4中出x2项，（1-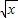
）3中出常数项，其系数为（-1）2C42×（-1）C3
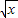=6，
②（1-x）4中出x项，（1-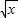
）3中出x项即
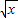的平方项，其系数为（-1）1C41×（-1）1C31
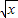=-12，
则其展开式中x2的系数是6-12=-6；
故答案为-6．
点评：本题考查二项式定理的应用，解题的关键是由因式乘法的运算法则，分析出得到x2项的情况．
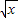）3的展开式的通项，由因式乘法法则分析可得要使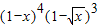的展开式中出现x2项，有2种情况，①（1-x）4中出x2项，（1-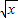）3中出常数项，②（1-x）4中出x项，（1-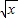）3中出x项即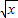的平方项，由二项式定理分别求出其系数，进而将其相加可得答案．解答：解：根据题意，（1-x）4的展开式的通项为Tr+1=C4r（-x）r=（-1）rC4r xr，
（1-
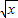）3的展开式的通项为Tr+1=C3r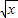（-）r=（-1）rC4r 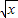r，要使
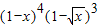的展开式中出现x2项，有2种情况，①（1-x）4中出x2项，（1-
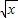）3中出常数项，其系数为（-1）2C42×（-1）C3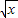=6，②（1-x）4中出x项，（1-
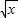）3中出x项即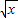的平方项，其系数为（-1）1C41×（-1）1C31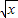=-12，则其展开式中x2的系数是6-12=-6；
故答案为-6．
点评：本题考查二项式定理的应用，解题的关键是由因式乘法的运算法则，分析出得到x2项的情况．
练习册系列答案
相关题目
(x+
)8的展开式中x2的系数是（ ）
| 2 |
| x |
| A、1120 | B、70 |
| C、56 | D、448 |