题目内容
设点F为椭圆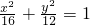 的左焦点,点P是椭圆上的动点.试求
的左焦点,点P是椭圆上的动点.试求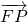 的模的最小值,并求此时点P的坐标.
的模的最小值,并求此时点P的坐标.
解:设P(x,y)为椭圆上的动点,由于椭圆方程为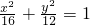 ,故-4≤x≤4.
,故-4≤x≤4.
由椭圆的方程可得:F(-2,0),
所以 ,
,
所以 =
= =
=
所以当x=-4时, 取得最小值.
取得最小值.
此时y=0,即P点的坐标为(-4,0).
分析:设P点的坐标为(x,y),由于椭圆方程为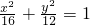 ,故-4≤x≤4.所以
,故-4≤x≤4.所以 ,所以
,所以 =
= ,
,
再利用二次函数的有关性质求出最值以及点P的坐标.
点评:本题主要考查了椭圆的性质与椭圆的基本知识的理解和应用,以及二次函数的简单性质.
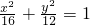 ,故-4≤x≤4.
,故-4≤x≤4.由椭圆的方程可得:F(-2,0),
所以
 ,
,所以
 =
= =
=
所以当x=-4时,
 取得最小值.
取得最小值.此时y=0,即P点的坐标为(-4,0).
分析:设P点的坐标为(x,y),由于椭圆方程为
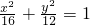 ,故-4≤x≤4.所以
,故-4≤x≤4.所以 ,所以
,所以 =
= ,
,再利用二次函数的有关性质求出最值以及点P的坐标.
点评:本题主要考查了椭圆的性质与椭圆的基本知识的理解和应用,以及二次函数的简单性质.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 上的一动点,F是椭圆的左焦点,
上的一动点,F是椭圆的左焦点, 的取值范围为
.
的取值范围为
.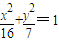 上的一动点,F是椭圆的左焦点,则|PF|的取值范围为 .
上的一动点,F是椭圆的左焦点,则|PF|的取值范围为 . 的左焦点,点P是椭圆上的动点.试求
的左焦点,点P是椭圆上的动点.试求 的模的最小值,并求此时点P的坐标.
的模的最小值,并求此时点P的坐标.