题目内容
已知不等式
对任意正实数x，y恒成立，则正实数a的最小值为 ．
【答案】分析：由题设知
≥16对于任意正实数x，y恒成立，所以1+a+
≥16，由此能求出正实数a的最小值．
解答：解：∵不等式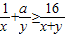
对任意正实数x，y恒成立，
∴
≥16对于任意正实数x，y恒成立
∵
=1+
≥1+a+2
，
∴1+a+
≥16
即
≥0，又a＞0，
从而
=9．
故答案为：9
点评：本题考查不等式的综合应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．
≥16对于任意正实数x，y恒成立，所以1+a+≥16，由此能求出正实数a的最小值．解答：解：∵不等式
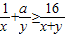对任意正实数x，y恒成立，∴
≥16对于任意正实数x，y恒成立∵
=1+≥1+a+2，∴1+a+
≥16 即
≥0，又a＞0，从而
=9．故答案为：9
点评：本题考查不等式的综合应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
既无最小值也无最大值；
上随机取一个数
，使得
成立的概率为
；
对任意正实数
恒成立，则正实数
的最小值为16；
，若方程
恰有三个不同的实根，则实数
的取值范围是
；以上正确的命题序号是：_______.
为极点，
轴的正半轴为极轴。已知点
的直角坐标为（1，-5），点
的极坐标为
若直线
过点
，圆
以
为半径。
先进行横坐标缩为原来的一半，纵坐标保持不变的伸缩变换，再做关于
对任意
无实根，求实数
的取值范围.
，2an+1=f（an）+15，bn=
（n∈N*）．已知不等式|f（x）≤2x2+4x-30|对任意实数x均成立．
）n]≤Sn＜2．