题目内容
设函数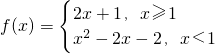 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是
- A.(-∞,-1)∪(1,+∞)
- B.(-∞,-1)∪[1,+∞)
- C.(-∞,-3)∪(1,+∞)
- D.(-∞,-3)∪[1,+∞)
B
分析:分x0≥1和x0<1两种情况考虑,分别将相应的函数解析式代入不等式中求出相应的解集,找出两解集的并集即为所求x0的取值范围.
解答:当x0≥1时,f(x0)=2x0+1,代入不等式得:2x0+1>1,
解得:x0>0,
此时x0的范围为x0≥1;
当x0<1时,f(x0)=x02-2x0-2,代入不等式得:x02-2x0-2>1,
解得:x0>3或x0<-1,
此时x0的范围为x0<-1,
综上,x0的取值范围是(-∞,-1)∪[1,+∞).
故选B
点评:此题考查了其他不等式的解法,利用了分类讨论的思想,是高考中常考的题型.
分析:分x0≥1和x0<1两种情况考虑,分别将相应的函数解析式代入不等式中求出相应的解集,找出两解集的并集即为所求x0的取值范围.
解答:当x0≥1时,f(x0)=2x0+1,代入不等式得:2x0+1>1,
解得:x0>0,
此时x0的范围为x0≥1;
当x0<1时,f(x0)=x02-2x0-2,代入不等式得:x02-2x0-2>1,
解得:x0>3或x0<-1,
此时x0的范围为x0<-1,
综上,x0的取值范围是(-∞,-1)∪[1,+∞).
故选B
点评:此题考查了其他不等式的解法,利用了分类讨论的思想,是高考中常考的题型.

练习册系列答案
相关题目
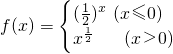 ,若f(x0)>2,则x0的取值范围是________.
,若f(x0)>2,则x0的取值范围是________.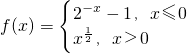 ,若f(x0)>1,则x0的取值范围是________.
,若f(x0)>1,则x0的取值范围是________.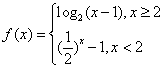 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是

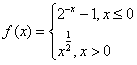 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是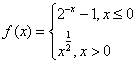 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是