题目内容
设函数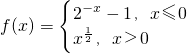
，若f（x0）＞1，则x0的取值范围是________．
（-∞，-1）∪（1，+∞）
分析：根据函数表达式分类讨论：①当x0≤0时，可得2-x-1＞1，得x＜-1；②当x0＞0时，x0.5＞1，可得x＞1，由此不难得出x0的取值范围是（-∞，-1）∪（1，+∞）．
解答：
①当x0≤0时，可得2-x0-1＞1，即2-x0＞2，所以-x0＞1，得x0＜-1；
②当x0＞0时，x00.5＞1，可得x0＞1．
故答案为（-∞，-1）∪（1，+∞）
点评：本题考查了基本初等函数的单调性和值域等问题，属于基础题．利用函数的单调性，结合分类讨论思想解题，是解决本题的关键．
分析：根据函数表达式分类讨论：①当x0≤0时，可得2-x-1＞1，得x＜-1；②当x0＞0时，x0.5＞1，可得x＞1，由此不难得出x0的取值范围是（-∞，-1）∪（1，+∞）．
解答：
①当x0≤0时，可得2-x0-1＞1，即2-x0＞2，所以-x0＞1，得x0＜-1；
②当x0＞0时，x00.5＞1，可得x0＞1．
故答案为（-∞，-1）∪（1，+∞）
点评：本题考查了基本初等函数的单调性和值域等问题，属于基础题．利用函数的单调性，结合分类讨论思想解题，是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
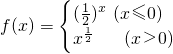，若f（x0）＞2，则x0的取值范围是________．
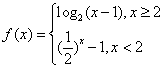，若f（x0）＞1，则x0的取值范围是
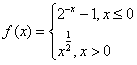，若f（x0）＞1，则x0的取值范围是
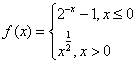，若f（x0）＞1，则x0的取值范围是