题目内容
已知数列 为其前n项和,计算得
为其前n项和,计算得 ,
, ,
, ,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
 为其前n项和,计算得
为其前n项和,计算得 ,
, ,
, ,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。解:推测 ,
,
证明:①“略”;
②假设n=k(k∈N*)时等式成立,即 ,
,
则



即n=k+1时,等式成立;
由①,②可知,对一切n∈N*,等式均成立。
 ,
,证明:①“略”;
②假设n=k(k∈N*)时等式成立,即
 ,
,则




即n=k+1时,等式成立;
由①,②可知,对一切n∈N*,等式均成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
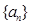 为等差数列,
为等差数列, 其前n项和,且
其前n项和,且 等于
等于